当前位置:
X-MOL 学术
›
Ind. Eng. Chem. Res.
›
论文详情
Our official English website, www.x-mol.net, welcomes your
feedback! (Note: you will need to create a separate account there.)
Capillary Condensation of Single- and Multicomponent Fluids in Nanopores
Industrial & Engineering Chemistry Research ( IF 3.8 ) Pub Date : 2019-10-03 , DOI: 10.1021/acs.iecr.9b04116 Gang Yang 1 , Di Chai 1 , Zhaoqi Fan 1, 2 , Xiaoli Li 1
Industrial & Engineering Chemistry Research ( IF 3.8 ) Pub Date : 2019-10-03 , DOI: 10.1021/acs.iecr.9b04116 Gang Yang 1 , Di Chai 1 , Zhaoqi Fan 1, 2 , Xiaoli Li 1
Affiliation
|
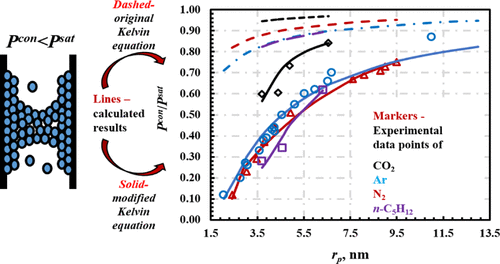
The phase behavior of fluids in nanopores deviates significantly from that in bulk space. However, the effect of pore confinement on the capillary condensation in nanopores has not been fully understood. In this work, the classic Kelvin equation is modified by incorporating the real gas effect, along with the pore size effect on the surface tension, the multilayer adsorption, and the molecule–wall interaction potential to improve its accuracy in calculating the capillary condensation pressure. The modified Kelvin equation is further extended for multicomponent fluids in nanopores. More specifically, an extended Peng–Robinson equation of state is applied to describe the real gas effect. The pore size effect on surface tension is reflected by accounting for the meniscus variation with pore size. The multilayer adsorption of both single- and multicomponent fluids are computed by the Brunauer–Emmett–Teller model, and the Frenkel–Halsey–Hill equation is used to calculate the molecule–wall interaction potential. Consequently, the modified Kelvin equation is validated with 42 collected experimental data, resulting in an overall relative deviation of 7.65 and 6.52% for single- and multicomponent fluids, respectively. It is also found that the molecule–wall interaction potential has the most significant contribution. Compared with the bulk condition, the capillary condensation pressure of CO2 at 265 K and the mixture CO2 + n-C5H12 + n-C6H14 at 390 K within 2 nm are predicted to be suppressed by 33.96 and 43.16%, respectively.
中文翻译:

纳米孔中单组分和多组分流体的毛细管冷凝
纳米孔中流体的相行为与大空间中的相行为显着不同。然而,尚未完全了解孔限制对纳米孔中的毛细管凝结的影响。在这项工作中,经典的Kelvin方程通过合并真实气体效应以及孔径对表面张力,多层吸附和分子-壁相互作用势的影响进行了修改,以提高其在计算毛细管冷凝压力时的准确性。修改后的开尔文方程式进一步扩展为纳米孔中的多组分流体。更具体地说,使用扩展的Peng-Robinson状态方程来描述真实的气体效应。孔径对表面张力的影响通过考虑弯月面随孔径的变化而反映出来。通过Brunauer-Emmett-Teller模型计算单组分和多组分流体的多层吸附,并使用Frenkel-Halsey-Hill方程计算分子与壁的相互作用势。因此,用42个收集的实验数据验证了修改后的开尔文方程,得出单组分和多组分流体的总相对偏差分别为7.65%和6.52%。还发现分子-壁相互作用的潜力是最重要的。与本体条件相比,CO的毛细管凝结压力 导致单组分和多组分流体的总相对偏差分别为7.65%和6.52%。还发现分子-壁相互作用的潜力是最重要的。与本体条件相比,CO的毛细管凝结压力 导致单组分和多组分流体的总相对偏差分别为7.65%和6.52%。还发现分子-壁相互作用的潜力是最重要的。与本体条件相比,CO的毛细管凝结压力265 K下的2和390 K下2 nm内的390 K下的CO 2 + n -C 5 H 12 + n -C 6 H 14混合物预计分别被抑制33.96和43.16%。
更新日期:2019-10-03
中文翻译:

纳米孔中单组分和多组分流体的毛细管冷凝
纳米孔中流体的相行为与大空间中的相行为显着不同。然而,尚未完全了解孔限制对纳米孔中的毛细管凝结的影响。在这项工作中,经典的Kelvin方程通过合并真实气体效应以及孔径对表面张力,多层吸附和分子-壁相互作用势的影响进行了修改,以提高其在计算毛细管冷凝压力时的准确性。修改后的开尔文方程式进一步扩展为纳米孔中的多组分流体。更具体地说,使用扩展的Peng-Robinson状态方程来描述真实的气体效应。孔径对表面张力的影响通过考虑弯月面随孔径的变化而反映出来。通过Brunauer-Emmett-Teller模型计算单组分和多组分流体的多层吸附,并使用Frenkel-Halsey-Hill方程计算分子与壁的相互作用势。因此,用42个收集的实验数据验证了修改后的开尔文方程,得出单组分和多组分流体的总相对偏差分别为7.65%和6.52%。还发现分子-壁相互作用的潜力是最重要的。与本体条件相比,CO的毛细管凝结压力 导致单组分和多组分流体的总相对偏差分别为7.65%和6.52%。还发现分子-壁相互作用的潜力是最重要的。与本体条件相比,CO的毛细管凝结压力 导致单组分和多组分流体的总相对偏差分别为7.65%和6.52%。还发现分子-壁相互作用的潜力是最重要的。与本体条件相比,CO的毛细管凝结压力265 K下的2和390 K下2 nm内的390 K下的CO 2 + n -C 5 H 12 + n -C 6 H 14混合物预计分别被抑制33.96和43.16%。































 京公网安备 11010802027423号
京公网安备 11010802027423号