当前位置:
X-MOL 学术
›
Nat. Commun.
›
论文详情
Our official English website, www.x-mol.net, welcomes your
feedback! (Note: you will need to create a separate account there.)
从双稳态折纸折叠成多稳态超曲面的离散几何的不变性和光滑极限。
Nature Communications ( IF 14.7 ) Pub Date : 2019-09-17 , DOI: 10.1038/s41467-019-11935-x
Ke Liu 1 , Tomohiro Tachi 2 , Glaucio H Paulino 3

"点击查看英文标题和摘要"
更新日期:2019-09-18
Nature Communications ( IF 14.7 ) Pub Date : 2019-09-17 , DOI: 10.1038/s41467-019-11935-x
Ke Liu 1 , Tomohiro Tachi 2 , Glaucio H Paulino 3
Affiliation
|
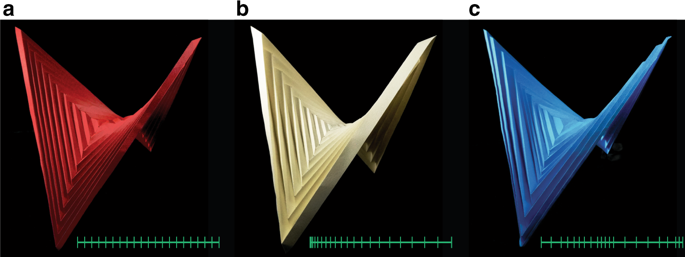
折纸提供了一种通过与尺寸无关的无损制造对三维形状进行编程的途径。尽管此类编程着重于单个瞬态下镶嵌的几何形状,但在此我们提供了从同心褶square正方形折叠平滑鞍形的完整描述。当图案的方形折痕之间的偏移是均匀的时,它被称为打褶的双曲线抛物面(hypar)折纸。尽管它很流行,但对于产生这种美学形状的机理仍然知之甚少。我们表明,从同心打褶的正方形折叠而来的优雅形状的数学极限,始终具有统一或不统一(例如,功能渐变,随机)偏移量,始终是双曲线抛物面。使用我们的理论模型将几何与力学联系起来,我们证明折叠的hypar折纸在两个对称构型之间表现出双稳性。此外,我们对hypar折纸进行细分,并利用其双稳态来对具有可编程非欧几里得几何形状的多稳定超表面进行编码。

"点击查看英文标题和摘要"


































 京公网安备 11010802027423号
京公网安备 11010802027423号