Capillary Flow in Open Microgrooves: Bifurcations and Networks.,Langmuir

当前位置： X-MOL 学术 › Langmuir › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

Capillary Flow in Open Microgrooves: Bifurcations and Networks.
Langmuir ( IF 3.7 ) Pub Date : 2019-07-18 00:00:00 , DOI: 10.1021/acs.langmuir.9b01456
Jing J Lee ₁ , Jean Berthier ₁ , Ashleigh B Theberge _{1,

2} , Erwin Berthier ₁

Affiliation

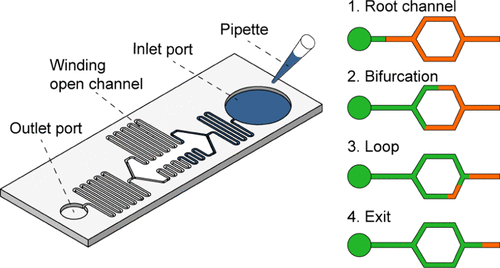
Open capillary flows are increasingly used in biotechnology, biology, thermics, and space science. So far, the dynamics of capillary flows has been studied mostly for confined channels. However, the theory of open microfluidics has considerably progressed during the last years, and an expression for the travel distance has been derived, generalizing the well-known theory of Lucas, Washburn, and Rideal. This generalization is based on the use of the average friction length and generalized Cassie angle. In this work, we successively study the spontaneous capillary flow in uniform cross section open rounded U-grooves—for which methods to determine the friction lengths are proposed—the flow behavior at a bifurcation, and finally flow in a simple-loop network. We show that after a bifurcation, the Lucas–Washburn–Rideal law needs to be adapted and the relation between the travel distance and time is more complicated than the square root of time dependency.

中文翻译：

开放式微槽中的毛细流动：分叉和网络。

开放的毛细管流越来越多地用于生物技术，生物学，热学和空间科学中。到目前为止，主要针对受限通道研究了毛细管流动的动力学。然而，在过去的几年中，开放式微流体理论取得了长足的进步，并通过归纳了Lucas，Washburn和Rideal的著名理论，得出了行进距离的表达式。该概括是基于平均摩擦长度和广义卡西角的使用。在这项工作中，我们先后研究了均匀横截面开口的圆形U形槽中的自发毛细管流（为此提出了确定摩擦长度的方法）在分叉处的流动行为，最后在单回路网络中流动。我们表明，在分叉之后，

更新日期：2019-07-18

点击分享查看原文

点击收藏

阅读更多本刊新发论文本刊介绍/投稿指南