Our official English website, www.x-mol.net, welcomes your
feedback! (Note: you will need to create a separate account there.)
Reassessment of the Four-Point Approach to the Electron-Transfer Marcus–Hush Theory
ACS Omega ( IF 3.7 ) Pub Date : 2018-02-21 00:00:00 , DOI: 10.1021/acsomega.7b01425 Omar López-Estrada 1 , Humberto G. Laguna 1 , Cihuapilli Barrueta-Flores 1 , Carlos Amador-Bedolla 1
ACS Omega ( IF 3.7 ) Pub Date : 2018-02-21 00:00:00 , DOI: 10.1021/acsomega.7b01425 Omar López-Estrada 1 , Humberto G. Laguna 1 , Cihuapilli Barrueta-Flores 1 , Carlos Amador-Bedolla 1
Affiliation
|
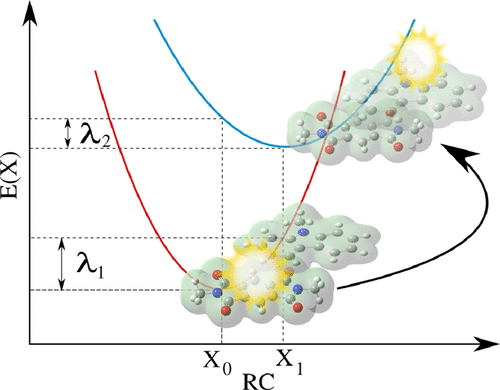
The Marcus–Hush theory has been successfully applied to describe and predict the activation barriers and hence the electron-transfer (ET) rates in several physicochemical and biological systems. This theory assumes that in the ET reaction, the geometry of the free Gibbs energy landscape is parabolic, with equal curvature near the local minimum for both reactants and products. In spite of its achievements, more realistic models have included the assumption of the two parabolas having not the same curvature. This situation is analyzed by the Nelsen’s four-point method. As a benchmark to compare the Marcus–Hush approximation to a precise calculation of the excitation energy, we studied the non-ET process of the electronic excitation of the aluminum dimer that has two local minima (3∑g– and 3∏u electronic states) and allows to obtain analytically the Marcus–Hush nonsymmetric parameters. We appraise the ability of the Marcus–Hush formula to approximate the analytical results by using several averages of the two reorganization energies associated with the forward and backward transitions and analyze the error. It is observed that the geometric average minimizes the relative error and that the analytical case is recovered. The main results of this paper are obtained by the application of the Nelsen’s four-point method to compute the reorganization energies of a large set of potential π-conjugated molecules proposed for organic photovoltaic devices using the above-mentioned averages for the Marcus–Hush formula. The activation energies obtained with the geometric average are significantly larger for some donor–acceptor pairs in comparison with the previously employed arithmetic average, their differences being suitable for experimental testing.
中文翻译:

电子转移马库斯-休斯理论的四点方法的重新评估
Marcus-Hush理论已成功地用于描述和预测活化障碍,从而描述和预测了几种物理化学和生物系统中的电子转移(ET)速率。该理论假设,在ET反应中,自由Gibbs能量态的几何形状是抛物线形,在反应物和产物的局部最小值附近均具有相等的曲率。尽管取得了一些成就,但更实际的模型包括两个抛物线曲率不相同的假设。通过Nelsen的四点方法分析了这种情况。为了比较Marcus-Hush近似值和精确计算激发能,作为基准,我们研究了具有两个局部最小值(3 ∑ g –和3 ∏ u电子状态),并允许解析地获得Marcus-Hush非对称参数。我们通过使用与向前和向后过渡相关的两个重组能量的几个平均值,评估Marcus-Hush公式近似分析结果的能力,并分析误差。可以看到,几何平均值使相对误差最小,并且分析情况得以恢复。本文的主要结果是通过应用尼尔森的四点方法,利用上述的马库斯-休斯公式的平均值计算有机光伏器件提出的大量潜在π-共轭分子的重组能而获得的。
更新日期:2018-02-21
中文翻译:

电子转移马库斯-休斯理论的四点方法的重新评估
Marcus-Hush理论已成功地用于描述和预测活化障碍,从而描述和预测了几种物理化学和生物系统中的电子转移(ET)速率。该理论假设,在ET反应中,自由Gibbs能量态的几何形状是抛物线形,在反应物和产物的局部最小值附近均具有相等的曲率。尽管取得了一些成就,但更实际的模型包括两个抛物线曲率不相同的假设。通过Nelsen的四点方法分析了这种情况。为了比较Marcus-Hush近似值和精确计算激发能,作为基准,我们研究了具有两个局部最小值(3 ∑ g –和3 ∏ u电子状态),并允许解析地获得Marcus-Hush非对称参数。我们通过使用与向前和向后过渡相关的两个重组能量的几个平均值,评估Marcus-Hush公式近似分析结果的能力,并分析误差。可以看到,几何平均值使相对误差最小,并且分析情况得以恢复。本文的主要结果是通过应用尼尔森的四点方法,利用上述的马库斯-休斯公式的平均值计算有机光伏器件提出的大量潜在π-共轭分子的重组能而获得的。






























 京公网安备 11010802027423号
京公网安备 11010802027423号