Cortical folding scales universally with surface area and thickness, not number of neurons,Science

当前位置： X-MOL 学术 › Science › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

Cortical folding scales universally with surface area and thickness, not number of neurons
Science ( IF 44.7 ) Pub Date : 2015-07-02 , DOI: 10.1126/science.aaa9101
Bruno Mota ₁ , Suzana Herculano-Houzel _{2,

3}

Affiliation

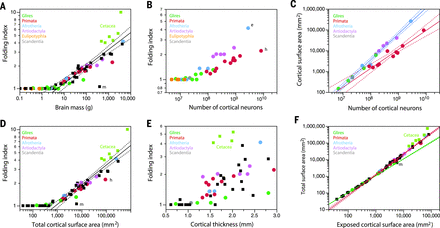
The best way to fold a mammalian brain As mammalian brains grew larger through evolution, the organization and folding of brains changed too. In a series of statistical analyses comparing a large number of mammalian species, Mota and Herculano-Houzel found that brain folding is not simply a phylogenetic consequence of brain mass increase (see the Perspective by Striedter and Srinivasan). The exposed surface of the cortex scales across all mammals and across individuals as a single power law of the product of total cortical surface and the square root of cortical thickness. Science, this issue p. 74; see also p. 31 A general physical rule governs brain folding across species and even individuals. [Also see Perspective by Striedter and Srinivasan] Larger brains tend to have more folded cortices, but what makes the cortex fold has remained unknown. We show that the degree of cortical folding scales uniformly across lissencephalic and gyrencephalic species, across individuals, and within individual cortices as a function of the product of cortical surface area and the square root of cortical thickness. This relation is derived from the minimization of the effective free energy associated with cortical shape according to a simple physical model, based on known mechanisms of axonal elongation. This model also explains the scaling of the folding index of crumpled paper balls. We discuss the implications of this finding for the evolutionary and developmental origin of folding, including the newfound continuum between lissencephaly and gyrencephaly, and for pathologies such as human lissencephaly.

中文翻译：

皮质折叠普遍与表面积和厚度有关，而不是神经元数量

折叠哺乳动物大脑的最佳方式随着哺乳动物大脑通过进化变得越来越大，大脑的组织和折叠也发生了变化。在比较大量哺乳动物物种的一系列统计分析中，Mota 和 Herculano-Houzel 发现大脑折叠不仅仅是大脑质量增加的系统发育结果（参见 Striedter 和 Srinivasan 的观点）。皮质的暴露表面在所有哺乳动物和个体之间缩放，作为总皮质表面和皮质厚度平方根的乘积的单一幂律。科学，这个问题 p。74; 另见第。31 一个通用的物理规则控制着跨物种甚至个体的大脑折叠。[另请参阅 Striedter 和 Srinivasan 的观点] 较大的大脑往往具有更多折叠的皮质，但皮质折叠的原因尚不清楚。我们表明，作为皮质表面积和皮质厚度平方根乘积的函数，皮质折叠程度在 lissencephalic 和 gyrencephalic 物种、个体之间和个体皮质内均匀分布。根据已知的轴突伸长机制，根据简单的物理模型，这种关系源自与皮质形状相关的有效自由能的最小化。该模型还解释了皱纸球折叠指数的缩放比例。我们讨论了这一发现对折叠的进化和发育起源的影响，包括新发现的无脑畸形和回脑畸形之间的连续体，以及人类无脑畸形等病理学。

更新日期：2015-07-02

点击分享查看原文

点击收藏

阅读更多本刊新发论文本刊介绍/投稿指南