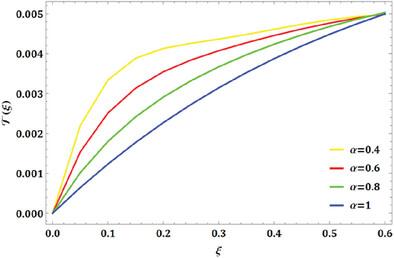
The manuscript investigates the numerical approximation of the fractional mathematical model of the financial crime population dynamics by the Gegenbauer wavelet collocation method. The study aims to enhance the accuracy and efficiency of solving the underlying differential equations that describe these phenomena by utilizing the proposed technique. The financial crime model is a nonlinear coupled system of ordinary differential equations. Using the Gegenbauer wavelets, the novel operational matrices of integration are created. A nonlinear system of ordinary differential equations are transformed into a system of algebraic equations using the characteristics of the Gegenbauer wavelet expansions and the operational matrix of integration, which speeds up processing. Then, this system of algebraic equations is solved using the Newton‐iterative technique to find the unknown Gegenbauer coefficients that help to obtain the approximate solution for the system. A numerical illustration is presented to show the efficacy and precision of the approach. The numerical results obtained from the projected approach are compared with the existing methods, such as NDSolve and Runge Kutta methods. These results show that the projected scheme is simple, reliable, and resilient. The findings suggest that this approach can be a powerful tool for researchers and practitioners in the financial sector, aiding in developing crime prevention and intervention strategies. The study concludes with suggestions for future research directions.

中文翻译：

---

使用 Gegenbauer 小波搭配法的分数阶金融犯罪模型研究


该手稿研究了通过 Gegenbauer 小波搭配方法对金融犯罪人口动态的分数数学模型的数值近似。该研究旨在通过利用所提出的技术来提高求解描述这些现象的基础微分方程的准确性和效率。金融犯罪模型是常微分方程的非线性耦合系统。使用 Gegenbauer 小波，创建了新的积分操作矩阵。利用 Gegenbauer 小波展开和积分运算矩阵的特性，将常微分方程的非线性方程组转换为代数方程组，从而加快处理速度。然后，使用牛顿迭代技术求解这个代数方程组，以找到有助于获得该系统的近似解的未知 Gegenbauer 系数。给出了一个数字说明来说明该方法的有效性和精度。将从投影方法获得的数值结果与现有方法（如 NDSolve 和 Runge Kutta 方法）进行比较。这些结果表明，投影方案简单、可靠且有弹性。研究结果表明，这种方法可以成为金融部门研究人员和从业者的有力工具，有助于制定犯罪预防和干预策略。该研究总结了对未来研究方向的建议。