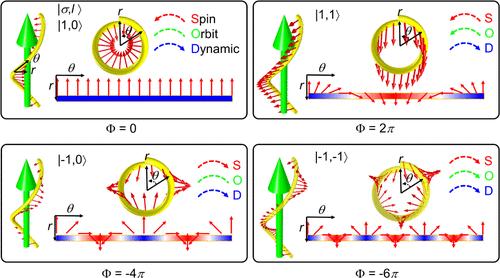
Understanding the interaction between light and chiral nanostructures is of fundamental importance, yet the principles governing chiral interactions have remained largely phenomenological. In this work, we present a chiral field-mode (FM) matching model to quantify the circular dichroism (CD) and helical dichroism (HD) of chiral plasmonic nanostructures interacting with beams of different spin–orbit states. The chiral FM matching model posits that among the inherent resonance modes within the nanostructure, the most efficiently excited mode is the one that matches the external field structure by possessing one more node along the vibration direction, with the field structure itself being determined by the interaction between the geometric phase and dynamic phase through a Doppler-like effect. The geometric phase in this model is well-defined by the product of the winding angle of the nanohelix and the angular momenta of light, including both its spin and orbital components. Thus, the beams of different spin–orbit states excite the specific resonance mode possessing one more node compared with the field structure, resulting in the spin-related CD and orbit-related HD. This model is extended to various chiral nanocomplexes, demonstrating how the field structure determines mode excitation and offering a comprehensive explanation for the CD and HD observed in various experimental setups. This model offers insights into the CD and HD microscopy in chiral nanostructures, contributing to the advancement of the fundamental theory of chiral nanophotonics.

中文翻译：

---

动态相位和几何相位之间的相互作用决定了圆二色性和螺旋二色性


了解光和手性纳米结构之间的相互作用至关重要，但支配手性相互作用的原理在很大程度上仍然是现象学的。在这项工作中，我们提出了一个手性场模式 （FM） 匹配模型，以量化手性等离子体纳米结构与不同自旋轨道状态的光束相互作用的圆二色性 （CD） 和螺旋二色性 （HD）。手性 FM 匹配模型假设，在纳米结构内的固有共振模式中，最有效的激发模式是通过沿振动方向拥有一个节点来匹配外部场结构的模式，场结构本身由几何相位和动态相位之间的相互作用通过多普勒样效应决定。该模型中的几何相位由纳米螺旋的缠绕角和光的角动量（包括其自旋和轨道分量）的乘积明确定义。因此，与场结构相比，不同自旋-轨道状态的光束激发了具有一个节点的特定共振模式，从而产生了自旋相关的 CD 和轨道相关的 HD。该模型扩展到各种手性纳米复合物，展示了场结构如何决定模式激发，并为在各种实验设置中观察到的 CD 和 HD 提供了全面的解释。该模型提供了对手性纳米结构中 CD 和 HD 显微镜的见解，有助于推进手性纳米光子学的基础理论。