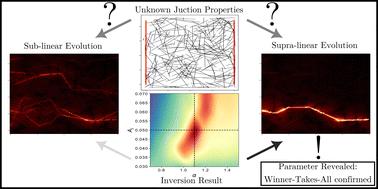
Random nanowire networks (NWNs) are interconnects that enable the integration of nanoscopic building blocks (the nanowires) in a disorganized fashion, enabling the study of complex emergent phenomena in nanomaterials and built-in fault-tolerant processing functionalities; the latter can lead to advances in large-scale electronic devices that can be fabricated with no particular array/grid high-precision pattern. However, when various nanowires are assembled to form an intricate network, their individual features are somehow lost in the complex NWN frame, in line with the complexity hallmark “the whole differs from the sum of the parts”. Individual nanowire materials and geometrical features can only be inferred indirectly by attempting to extract information about their initial conditions from a response function measurement. In this work, we present a mathematical framework that enables inference of the intrinsic properties of highly complex/intricate systems such as random NWNs in which information about their individual parts cannot be easily accessed due to their network formation and dynamical conductance behaviour falling in the category of memristive systems. Our method, named misfit minimization, is rooted in nonlinear regression supervised learning approaches in which we find the optimum parameters that minimize a cost function defined as the square least error between conductance evolution curves taken for a target NWN system and multiple configurational NWN samples composing the training set. The optimized parameters are features referent to the target NWN system's initial conditions obtained in an inverse fashion: from the response output function, we extract information about the target system's initial conditions. Accessing the nanowire individual features in a NWN frame, as our methodology allows, enables us to predict the conduction mechanisms of the NWN subjected to a current input source; these can be via a “winner-takes-all” energy-efficient scheme using a single conduction pathway composed of multiple nanowires connected in series or via multiple parallel conduction pathways. Predicting the conduction mechanism of complex and dynamical systems such as memristive NWNs is critical for their use in next-generation memory and brain-inspired technologies since their memory capability relies on the creation of such pathways activated and consolidated by the input current signal.

中文翻译：

---

识别随机纳米线网络中的赢家通吃出现：一个逆问题


随机纳米线网络 （NWN） 是一种互连，能够以杂乱无章的方式集成纳米级构建块（纳米线），从而能够研究纳米材料中复杂的新兴现象和内置的容错处理功能;后者可以导致大规模电子设备的进步，这些器件可以在没有特定阵列/网格高精度图案的情况下制造。然而，当各种纳米线组装成一个复杂的网络时，它们的各个特征在复杂的 NWN 框架中以某种方式丢失了，这与“整体不同于部分之和”的复杂性特征一致。单个纳米线材料和几何特征只能通过尝试从响应函数测量中提取有关其初始条件的信息来间接推断。在这项工作中，我们提出了一个数学框架，该框架能够推断高度复杂/错综复杂的系统（例如随机 NWN）的内在特性，其中由于它们的网络形成和动态电导行为属于忆阻系统类别，因此无法轻松访问有关其各个部分的信息。我们的方法名为 misfit minimization，植根于非线性回归监督学习方法，其中我们找到最小化成本函数的最佳参数，该成本函数定义为为目标 NWN 系统采用的电导演变曲线与构成训练集的多个配置 NWN 样本之间的平方最小误差。优化后的参数是与目标 NWN 系统的初始条件相关的特征，以相反的方式获得：从响应输出函数中，我们提取有关目标系统初始条件的信息。 在我们的方法允许的情况下，访问 NWN 框架中的纳米线单个特征，使我们能够预测受电流输入源影响的 NWN 的传导机制;这些可以通过“赢家通吃”的节能方案来实现，该方案使用由多个串联的纳米线组成的单个传导路径，或通过多个并联导电路径组成。预测忆阻 NWN 等复杂和动态系统的传导机制对于它们在下一代记忆和类脑技术中的使用至关重要，因为它们的记忆能力依赖于由输入电流信号激活和巩固的此类路径的创建。