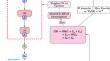
Machine learning, particularly neural networks, has rapidly permeated most activities and work where data has a story to tell. Recently, deep learning has started to be used for solving differential equations with input from physics, also known as Physics-Informed Neural Network (PINNs). Physics-Informed Neural Networks (PINNs) applications in numerical relativity remain mostly unexplored. To remedy this situation, we present the first study of applying PINNs to solve in the time domain the Zerilli and the Regge-Wheeler equations for Schwarzschild black hole perturbations. The fundamental difference of our work with other PINN studies in black hole perturbations is that, instead of working in the frequency domain, we solve the equations in the time domain, an approach commonly used in numerical relativity to study initial value problems. To evaluate the accuracy of PINNs results, we compare the extracted quasi-normal modes with those obtained with finite difference methods. For comparable grid setups, the PINN results are similar to those from finite difference methods and differ from those obtained in the frequency domain by a few percent. As with other applications of PINNs for solving partial differential equations, the efficiency of neural networks over other methods emerges when applied to large dimensionality or high complexity problems. Our results support the viability of PINNs in numerical relativity, but more work is needed to assess their performance in problems such as the collision of compact objects.

机器学习，尤其是神经网络，已经迅速渗透到大多数数据有故事的活动和工作中。最近，深度学习已开始用于使用物理学输入求解微分方程，也称为物理信息神经网络 （PINN）。物理信息神经网络 （PINN） 在数值相对论中的应用仍未得到探索。为了解决这种情况，我们提出了第一个应用 PINN 在时域中求解 Schwarzschild 黑洞扰动的 Zerilli 和 Regge-Wheeler 方程的研究。我们在黑洞扰动中与其他 PINN 研究的根本区别在于，我们不是在频域中工作，而是在时域中求解方程，这是数值相对论中常用的一种方法来研究初始值问题。为了评估 PINNs 结果的准确性，我们将提取的准正态模式与使用有限差分方法获得的准正态模式进行了比较。对于类似的网格设置，PINN 结果与有限差分方法的结果相似，与在频域中获得的结果相差几个百分点。与 PINN 用于求解偏微分方程的其他应用一样，当应用于大维度或高复杂性问题时，神经网络的效率优于其他方法。我们的结果支持 PINN 在数值相对论中的可行性，但需要更多的工作来评估它们在紧凑物体碰撞等问题中的表现。