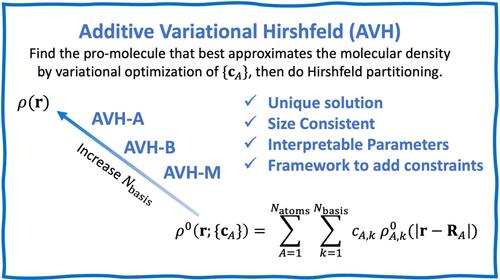
We introduce the general mathematical framework of variational Hirshfeld partitioning, wherein the best possible approximation to a molecule’s electron density is obtained by minimizing the f-divergence between the molecular density and a non-negative linear combination of (normalized) basis functions. This framework subsumes several existing methods that variationally optimize their pro-atoms, like (Gaussian) iterative stockholder analysis (ISA and GISA) and minimal basis iterative stockholder partitioning (MBIS), and provides a solid foundation for developing mathematically rigorous partitioning schemes. In this paper, we delve into the mathematical underpinnings of Hirshfeld-inspired partitioning schemes and show that among all the valid f-divergence measures only the extended Kullback–Leibler is a suitable choice. This led us to develop a novel partitioning scheme, called additive variational Hirshfeld (AVH), which constructs the pro-molecular density as a convex linear combination of the densities from selected states of isolated atoms and atomic ions. The AVH method is size-consistent with a unique solution and provides a straightforward approach for adding constraints for fragment properties. It also results in an intuitively appealing valence-bond-like decomposition of the molecular density as a weighted average of the densities of the atomic states in the molecule; that is, the AVH atomic density is a minimal deformation of the corresponding isolated atomic reference state’s density. Compared to other variational Hirshfeld variants, our numerical results show that AVH yields chemically interpretable and sensible atomic charges that are not excessively large and demonstrate computational robustness.

中文翻译：

---

变分 Hirshfeld 分区：一般框架和加法变分 Hirshfeld 分区方法


我们介绍了变分 Hirshfeld 分配的一般数学框架，其中分子电子密度的最佳近似值是通过最小化分子密度与（归一化）基函数的非负线性组合之间的 f 发散来获得的。该框架包含几种现有的方法，这些方法以可变方式优化其前原子，如（高斯）迭代股东分析（ISA 和 GISA）和最小基迭代股东分区 （MBIS），并为开发数学上严格的分区方案提供了坚实的基础。在本文中，我们深入研究了受 Hirshfeld 启发的分区方案的数学基础，并表明在所有有效的 f 散度度量中，只有扩展的 Kullback-Leibler 是合适的选择。这导致我们开发了一种新的分配方案，称为加性变分 Hirshfeld （AVH），它将前分子密度构建为孤立原子和原子离子的选定状态的密度的凸线性组合。AVH 方法的大小与独特的解决方案一致，并为片段属性添加约束提供了一种简单的方法。它还导致分子密度的直观上吸引人的价键样分解，作为分子中原子态密度的加权平均值;也就是说，AVH 原子密度是相应孤立原子参考态密度的最小变形。与其他变分 Hirshfeld 变体相比，我们的数值结果表明，AVH 产生化学上可解释和合理的原子电荷，这些原子电荷不会太大，并表现出计算鲁棒性。