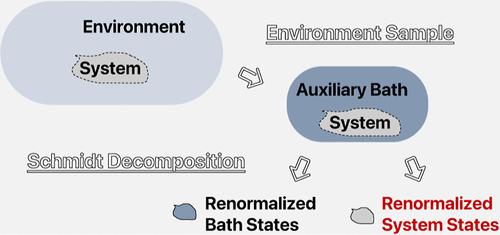
The strength of the density matrix renormalization group (DMRG) in handling strongly correlated systems lies in its unbiased and simultaneous treatment of identical sites that are both energetically degenerate and spatially similar, as typically encountered in physical models. However, this very feature becomes a drawback when DMRG is applied to quantum chemistry calculations for large, realistic correlated systems. This is because entangled orbitals often span broad ranges in both energy and space, with their interactions being notably inhomogeneous. In this study, we suggest addressing the strong intrafragment correlations and weak interfragment correlations separately, utilizing a large-scale multiconfigurational calculation framework grounded in the block interaction product state formulation. The strong intrafragment correlation can be encapsulated in several electronic states located on fragments, which are obtained by considering the entanglement between fragments and their environments. Moreover, we incorporate non-Abelian spin-SU(2) symmetry in our work to target the desired states we interested with well-defined particle number and spin, providing deeper insights into the corresponding chemical processes. The described method has been examined in various chemical systems and demonstrates high efficiency in addressing the inhomogeneous effects in strong correlation quantum chemistry.

中文翻译：

---

使用块交互产品状态对非均匀相关系统进行高效仿真


密度矩阵重整化群 （DMRG） 在处理强相关系统方面的优势在于，它无偏且同时处理能量退化和空间相似的相同位点，这在物理模型中通常遇到。然而，当 DMRG 应用于大型、现实相关系统的量子化学计算时，这一功能就变成了一个缺点。这是因为纠缠轨道通常在能量和空间上跨越很宽的范围，它们的相互作用明显不均匀。在本研究中，我们建议利用基于块相互作用产物状态公式的大规模多配置计算框架，分别处理强片段内相关性和弱片段间相关性。强片段内相关性可以封装在位于片段上的几种电子状态中，这些电子态是通过考虑片段与其环境之间的纠缠获得的。此外，我们将非阿贝尔自旋 SU（2） 对称性纳入我们的工作中，以明确定义的粒子数和自旋来靶向我们感兴趣的所需状态，从而更深入地了解相应的化学过程。所描述的方法已经在各种化学系统中进行了检查，并证明了在解决强相关量子化学中的不均匀效应方面的高效性。