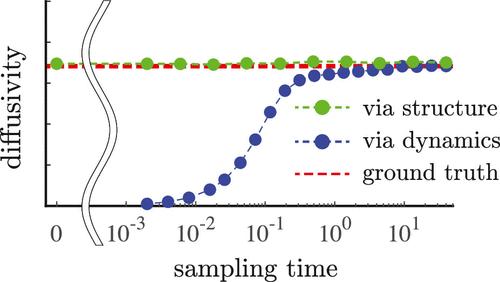
In molecular-dynamics simulations of fluids, the Einstein–Helfand (EH) and Green–Kubo (GK) relationships are frequently used to compute a variety of transport coefficients, including diffusion coefficients. These relationships are formally valid in the limit of infinite sampling time: The error in the estimate of a transport coefficient (relative to an infinitely long simulation) asymptotically approaches zero as more dynamics are simulated and recorded. In practice, of course, one can only simulate a finite number of particles for a finite amount of time. In this work, we show that in this pre-asymptotic regime, an approach for estimating diffusion coefficients based upon excess entropy scaling (EES) achieves a significantly lower error than either EH or GK relationships at fixed online sampling time. This approach requires access only to structural information at the level of the radial distribution function (RDF). We further demonstrate that the use of a recently developed RDF mollification scheme significantly reduces the amount of sampling time needed to converge to the long-time value of the diffusion coefficient. We also demonstrate favorable sample-to-sample variances in the diffusion coefficient estimate obtained using EES as compared to those obtained using EH and GK.

中文翻译：

---

一张图片胜过一千个时间步长：用于快速估计流体分子动力学模拟中扩散系数的超熵标度


在流体的分子动力学仿真中，Einstein-Helfand （EH） 和 Green-Kubo （GK） 关系经常用于计算各种输运系数，包括扩散系数。这些关系在无限采样时间的限制下正式有效：随着仿真和记录的动力学增加，传输系数估计的误差（相对于无限长的仿真）逐渐接近零。当然，在实践中，人们只能在有限的时间内模拟有限数量的粒子。在这项工作中，我们表明，在这种预渐近状态下，基于超额熵缩放 （EES） 估计扩散系数的方法在固定在线采样时间内实现的误差明显低于 EH 或 GK 关系。这种方法只需要访问径向分布函数 （RDF） 级别的结构信息。我们进一步证明，使用最近开发的 RDF 柔和方案显着减少了收敛到扩散系数的长时间值所需的采样时间。我们还证明，与使用 EH 和 GK 获得的扩散系数估计相比，使用 EES 获得的扩散系数估计存在有利的样本间差异。