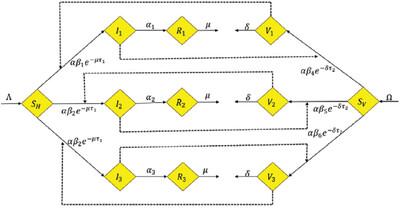
This study presents a comprehensive mathematical model to analyze the dynamics of co‐infection between dengue and malaria using delay differential equations. The model investigates the transmission dynamics of both diseases, focusing on the stability of equilibrium points and the basic reproductive ratio, which measures the number of secondary infections caused by a single infected individual. A time‐delay component is incorporated to account for the incubation periods, enhancing the model's realism. The study performs a detailed sensitivity analysis and global stability assessments, providing insights into the control and management of diseases. Numerical simulations are conducted to illustrate the effect of various transmission parameters on disease spread. This research highlights the importance of mathematical modeling in understanding co‐infection dynamics and provides critical insights for public health interventions, particularly in regions where both diseases are endemic. The results emphasize the role of controlling transmission rates and the use of vector management strategies in mitigating disease outbreaks.

中文翻译：

---

使用延迟微分方程对登革热和疟疾的共同感染动力学进行数学建模


本研究提出了一个全面的数学模型，使用延迟微分方程分析登革热和疟疾之间合并感染的动态。该模型研究了两种疾病的传播动力学，重点关注平衡点的稳定性和基本繁殖率，后者衡量单个感染者引起的继发感染数量。加入时间延迟组件以考虑孵化期，从而增强模型的真实感。该研究进行了详细的敏感性分析和整体稳定性评估，为疾病的控制和管理提供了见解。进行数值模拟以说明各种传播参数对疾病传播的影响。这项研究强调了数学建模在理解合并感染动态方面的重要性，并为公共卫生干预提供了关键见解，特别是在这两种疾病都流行的地区。结果强调了控制传播率和使用病媒管理策略在减轻疾病爆发中的作用。