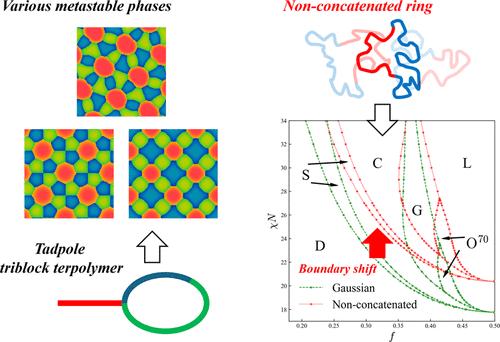
We propose an efficient method for the self-assembly of Gaussian block copolymers with general cyclic architectures and nonconcatenated ring block copolymer in a melt based on a Ginzburg–Landau-type density functional theory combined with random phase approximation. For the Gaussian copolymers, the applicability of the density functional theory is enhanced by a Gaussian embedding method with a graph Laplacian, which allows evaluating single-chain scattering functions for arbitrary architectures including internal multicycles without analytical difficulty. By using this methodology, we predict phase diagrams of ring and bicycle diblock copolymers at the same cost as a linear diblock copolymer, and discover various metastable morphologies of a tadpole triblock terpolymer, which have not been observed for linear and star triblock terpolymers. We also demonstrate that our framework predicts the phase diagram of the nonconcatenated ring diblock copolymer with the aid of its single-chain scattering function obtained by experiments.

中文翻译：

---

环状嵌段共聚物熔体的密度泛函理论


我们提出了一种基于 Ginzburg-Landau 型密度泛函理论结合随机相位近似的高斯嵌段共聚物和非串联环嵌段共聚物在熔体中自组装的有效方法。对于高斯共聚物，密度泛函理论的适用性通过带有图拉普拉斯分布量的高斯嵌入方法得到增强，该方法允许评估任意架构（包括内部多周期）的单链散射函数，而不会产生分析困难。通过使用这种方法，我们以与线性二嵌段共聚物相同的成本预测了环和自行车二嵌段共聚物的相图，并发现了蝌蚪三嵌段三元共聚物的各种亚稳态形态，而线性和星形三嵌段共聚物则没有观察到这些形态。我们还证明，我们的框架借助实验获得的单链散射函数预测了非串联环二嵌段共聚物的相图。