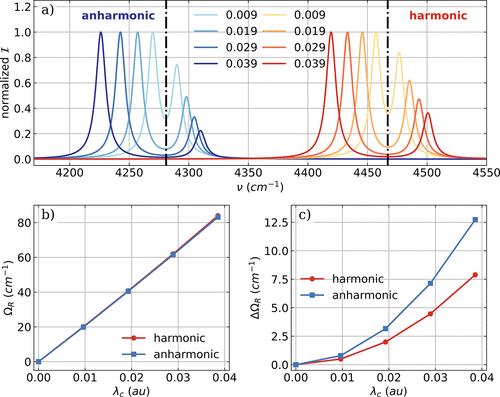
Recently, we have discovered several errors in our paper “Ab Initio Vibro-Polaritonic Spectra in Strongly Coupled Cavity-Molecule Systems” [Schnappinger and Kowalewski J. Chem. Theory Comput. 2023, 19, 9278] which we would like to correct here. The expression of the infrared (IR) intensity ℐ𝐻𝑖${{}^H\mathcal{I}}_i$${{}^H\mathcal{I}}_i$ for the harmonic approximation given in eq 15 is lacking the atomic masses and should read instead Figure 1. a) Vibro-polaritonic IR spectra of a single HF molecule calculated in the harmonic approximation (reddish) and in the full-quantum setup (bluish), individually normalized for each coupling strength. The black dashed dotted lines indicate the bare molecular frequencies of the fundamental transitions of the harmonic case (^Hν₁ = 4467 cm^–1) and the anharmonic case (^Aν₁ = 4281 cm^–1). The cavity frequency ω_c is resonant with the corresponding fundamental transition, and the coupling strength λ_c increases from 0.009 au to 0.039 au (from lightest to darkest color). The Rabi splitting Ω_R (b) and its asymmetry ΔΩ_R =ω_c – 0.5(ν^LP+ν^UP) (c) as a function of λ_c. Figure 4. a) Vibro-polaritonic IR spectra of a single HF molecule calculated in the harmonic approximation (reddish) and in the full-quantum setup (bluish), individually normalized for each coupling strength. In both cases, the full SCF treatment is neglected; for details, see text. Black dashed-dotted lines indicate the frequencies of the harmonic fundamental transition (^Hν₁ = 4467 cm^–1) and the anharmonic fundamental transition (^Aν₁ = 4281 cm^–1). The cavity frequency ω_c is resonant with the corresponding fundamental transition in both cases, and the coupling strength λ_c increases from 0.009 au to 0.039 au (from light to dark color). b) Rabi splitting Ω_R as a function of λ_c. c) Asymmetry ΔΩ_R = ω_c – 0.5(ν^LP+ν^UP) of the Rabi splitting. Figure 5. Vibro-polaritonic IR spectra calculated in the harmonic approximation for different numbers of HF molecules (color-coded) shown with respect to the cavity frequency ω_c. The cavity is resonant with the harmonic fundamental transition (^Hν₁ = 4467 cm^–1, black dashed-dotted lines) and a rescaled coupling strength of λ₀ of 0.057 au is used (see eq 17). a) Full CBO-HF simulation in the all-parallel configuration. b) Full CBO-HF simulation in the antiparallel configuration. c) Linear CBO-HF simulation (without DSE terms) in the all-parallel configuration. c) Linear CBO-HF simulation (without DSE terms) in the antiparallel configuration. Figure 7. a) Vibronic IR spectra of a single NH₃ molecule calculated in the harmonic approximation. The low energy part of the vibro-polaritonic IR spectra of a single NH₃ molecule zoomed into the symmetric mode (b,d) and the two asymmetric bending modes shown in (c,e). The polarization axis of the cavity mode is the y axis for (b,c) and equal to the z axis for (d,e). The cavity frequency ω_c is resonant with the symmetric bending mode (1103 cm^–1) and the cavity field strength λ_c increases from 0.039 au to 0.155 au. The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.4c01374. Corrected Figures S3, S4, and S13 (PDF) Correction to Ab Initio Vibro-Polaritonic Spectra in Strongly Coupled Cavity-Molecule Systems 3 views 0 shares 0 downloads Most electronic Supporting Information files are available without a subscription to ACS Web Editions. Such files may be downloaded by article for research use (if there is a public use license linked to the relevant article, that license may permit other uses). Permission may be obtained from ACS for other uses through requests via the RightsLink permission system: http://pubs.acs.org/page/copyright/permissions.html. This article has not yet been cited by other publications.

中文翻译：

---

在强耦合腔-分子系统中对 Ab Initio Vibro-Polaritonic 光谱的校正


最近，我们在论文“强耦合腔-分子系统中的 Ab Initio Vibro-Polaritonic Spectra”中发现了几个错误 [Schnappinger 和 Kowalewski J. Chem. Theory Comput.2023， 19， 9278] 我们想在这里更正。红外 （IR） 强度的表达式ℐ𝐻 我${{}^H\mathcal{I}}_i$${{}^H\mathcal{I}}_i$
因为方程 15 中给出的谐波近似值缺少原子质量，应改为图 1。a） 在谐波近似（偏红）和全量子设置（偏蓝）中计算的单个 HF 分子的振极-偏振红外光谱，并针对每个耦合强度单独归一化。黑色虚线表示谐波情况 （^Hν₁ = 4467 cm^–1） 和非谐波情况 （^Aν₁ = 4281 cm^–1） 的基跃的裸分子频率。腔频率 ω_c 与相应的基跃相谐振，耦合强度 λ_c 从 0.009 au 增加到 0.039 au（从最浅的颜色到最暗的颜色）。拉比分裂 Ω_R （b） 及其不对称性 ΔΩ_R =ω_c – 0.5（ν^LP+ν^UP） （c） 作为 λ_c 的函数。图 4.a） 在谐波近似（偏红）和全量子设置（偏蓝）中计算的单个 HF 分子的振极-偏振红外光谱，并针对每个耦合强度单独归一化。在这两种情况下，都忽略了完整的 SCF 治疗;有关详细信息，请参阅文本。黑色虚线表示谐波基频跃迁 （^Hν₁ = 4467 cm^–1） 和非谐波基频跃迁 （^Aν₁ = 4281 cm^–1） 的频率。在这两种情况下，腔频率 ω_c 都与相应的基波跃迁谐振，耦合强度 λ_c 从 0.009 au 增加到 0.039 au（从浅色到深色）。 b） Rabi 分裂 Ω_R 与 λ_c 的函数关系。c） 拉比分裂的不对称性 ΔΩ_R = ω_c – 0.5（ν^LP+ν^UP）。图 5.振动偏振子红外光谱，以不同数量的 HF 分子（颜色编码）的谐波近似计算，显示相对于腔体频率 ω_c。腔体与谐波基波跃迁（^Hν₁ = 4467 cm^–1，黑色虚线）谐振，并使用 0.057 au 的 λ₀ 重新缩放的耦合强度（见方程 17）。a） 全并行配置中的全 CBO-HF 仿真。b） 反并行配置中的全 CBO-HF 仿真。c） 全并行配置中的线性 CBO-HF 仿真（无 DSE 项）。c） 反并行配置中的线性 CBO-HF 模拟（无 DSE 项）。图 7.a） 以谐波近似计算的单个 NH₃ 分子的振动红外光谱。单个 NH₃ 分子的振动偏振红外光谱的低能量部分放大到对称模式 （b，d） 和 （c，e） 中所示的两种不对称弯曲模式。腔模式的极化轴是 （b，c） 的 y 轴，等于 （d，e） 的 z 轴。腔频率 ω_c 与对称弯曲模式 （1103 cm^–1） 谐振，腔体场强 λ_c 从 0.039 au 增加到 0.155 au。支持信息可在 https://pubs.acs.org/doi/10.1021/acs.jctc.4c01374 免费获取。更正后的图 S3、S4 和 S13 （PDF） 对 Ab 的校正 Initio 振动-偏振子光谱 在 强耦合腔分子系统中 3 视图 0 分享 0 下载 大多数电子支持信息文件无需订阅 ACS Web Editions 即可获得。此类文件可以按文章下载用于研究用途（如果有链接到相关文章的公共使用许可证，则该许可证可能允许其他用途）。可以通过 RightsLink 权限系统（http://pubs.acs.org/page/copyright/permissions.html）请求，从 ACS 获得用于其他用途的权限。本文尚未被其他出版物引用。