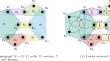
Planar hypergraphs are widely used in several applications, including VLSI design, metro maps, information visualisation, and databases. The minimum \( s-t \) hypercut problem in a weighted hypergraph is to find a partition of the vertices into two nonempty sets, S and \( \overline{S} \), with \(s\in S\) and \(t\in \overline{S}\) that minimizes the total weight of hyperedges that have at least two endpoints in two different sets. In the present study, we propose an approach that effectively solves the minimum \( s-t \) hypercut problem in (s, t)-planar hypergraphs. The method proposed demonstrates polynomial time complexity, providing a significant advancement in solving this problem. The modelling example shows that the proposed strategy is effective at obtaining balanced bipartitions in VLSI circuits.

平面超图广泛用于多种应用，包括 VLSI 设计、地铁地图、信息可视化和数据库。加权超图中的最小 \（ s-t \） 超切割问题是找到顶点分为两个非空集，S 和 \（ \overline{S} \），其中 \（s\in S\） 和 \（t\in \overline{S}\） 最小化在两个不同集合中至少有两个端点的超边的总权重。在本研究中，我们提出了一种有效解决 （s， t） 平面超图中最小 \（ s-t \） 超切问题的方法。所提出的方法证明了多项式时间复杂度，为解决这个问题提供了重大进步。建模示例表明，所提出的策略在获得 VLSI 电路中的平衡双分区方面是有效的。