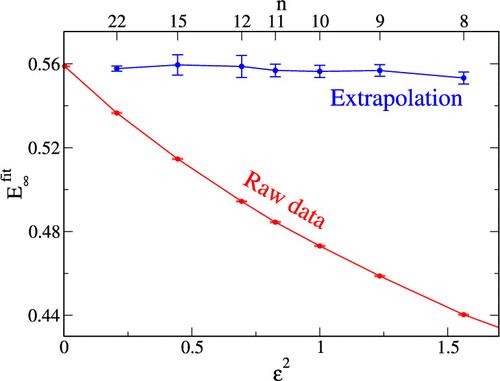
Convergence of imaginary-time path integral results requires a substantial number of beads (n) when quantum effects are significant. Traditional Trotter scaling approaches estimate the continuum limit (n → ∞) through extrapolation; however, their validity is restricted to the asymptotic domain of large n. We introduce an efficient extrapolation approach for quantum oscillators and crystals with harmonic character. The fitting function is inspired by the analytic solution of the harmonic oscillator (HO), or the Einstein crystal for solids. While the formulation is designed for first derivative properties (energy and pressure), its extension to second derivative properties (e.g., heat capacity) is straightforward. We apply the method to a one-dimensional HO and anharmonic oscillator (AO), as well as a three-dimensional Lennard-Jones crystal. Configurations are sampled using path integral molecular dynamics simulations in the canonical ensemble, at a low temperature of T = 0.1 (simulation units). Compared to Trotter extrapolation approaches, the new method demonstrates a substantial accuracy in estimating the continuum limit, using only a few simulations of relatively small system sizes. This efficiency significantly reduces computational cost, providing a powerful tool to facilitate computations for more complex and challenging systems, such as molecules and crystals modeled using ab initio methods.

中文翻译：

---

在量子振荡器和晶体的路径积分模拟中准确快速地估计连续极限


当量子效应显著时，虚时路径积分结果的收敛需要大量的珠子 （n）。传统的 Trotter 缩放方法通过外推估计连续体极限 （n → ∞）;然而，它们的有效性仅限于大 N 的渐近域。我们为具有谐波特性的量子振荡器和晶体引入了一种有效的外推方法。拟合函数的灵感来自谐振子 （HO） 或固体爱因斯坦晶体的解析解。虽然该公式是针对一阶导数性质（能量和压力）设计的，但它扩展到二阶导数性质（例如热容）很简单。我们将该方法应用于一维 HO 和非谐振荡器 （AO） 以及三维 Lennard-Jones 晶体。在 T = 0.1 的低温（模拟单位）下，使用规范集合中的路径积分分子动力学模拟对构型进行采样。与 Trotter 外推方法相比，新方法在估计连续谱极限方面表现出相当大的准确性，仅使用少数相对较小的系统大小的模拟。这种效率显著降低了计算成本，为更复杂和更具挑战性的系统（例如使用 ab initio 方法建模的分子和晶体）提供了强大的工具。