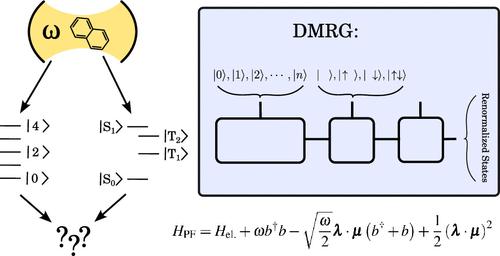
The emerging field of polaritonic chemistry explores the behavior of molecules under strong coupling with cavity modes. Despite recent developments in ab initio polaritonic methods for simulating polaritonic chemistry under electronic strong coupling, their capabilities are limited, especially in cases where the molecule also features strong electronic correlation. To bridge this gap, we have developed a novel method for cavity QED calculations utilizing the Density Matrix Renormalization Group (DMRG) algorithm in conjunction with the Pauli–Fierz Hamiltonian. Our approach is applied to investigate the effect of the cavity on the S₀–S₁ transition of n-oligoacenes, with n ranging from 2 to 5, encompassing 22 fully correlated π orbitals in the largest pentacene molecule. Our findings indicate that the influence of the cavity intensifies with larger acenes. Additionally, we demonstrate that, unlike the full determinantal representation, DMRG efficiently optimizes and eliminates excess photonic degrees of freedom, resulting in an asymptotically constant computational cost as the photonic basis increases.

中文翻译：

---

使用密度矩阵重整化组方法的极化化学


极化子化学的新兴领域探索了分子在与空腔模式的强耦合下的行为。尽管在电子强耦合下模拟偏振子化学的从头极化方法最近取得了进展，但它们的能力是有限的，尤其是在分子也具有强电子相关性的情况下。为了弥合这一差距，我们开发了一种利用密度矩阵重整化组 （DMRG） 算法和 Pauli-Fierz 哈密顿量计算腔 QED 的新方法。我们的方法用于研究空腔对 n-寡乙烷的 S_{0-S 1} 转变的影响，n 范围为 2 到 5，在最大的五聚烯分子中包含 22 个完全相关的 π 轨道。我们的研究结果表明，空腔的影响随着乙酮的增大而增强。此外，我们还证明，与完全行列式表示不同，DMRG 有效地优化和消除了多余的光子自由度，随着光子基的增加，导致渐近恒定的计算成本。