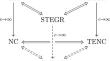
The geometric trinity of gravity comprises three distinct formulations of general relativity: (i) the standard formulation describing gravity in terms of spacetime curvature, (ii) the teleparallel equivalent of general relativity describing gravity in terms of spacetime torsion, and (iii) the symmetric teleparallel equivalent of general relativity (STEGR) describing gravity in terms of spacetime non-metricity. In this article, we complete a geometric trinity of non-relativistic gravity, by (a) taking the non-relativistic limit of STEGR to determine its non-relativistic analogue, and (b) demonstrating that this non-metric theory is equivalent to Newton–Cartan theory and its teleparallel equivalent, i.e., the curvature and the torsion based non-relativistic theories that are both geometrised versions of classical Newtonian gravity.

引力的几何三位一体包括广义相对论的三种不同表述：（i） 用时空曲率描述引力的标准公式，（ii） 用时空扭转描述引力的广义相对论的远平行等价物，以及 （iii） 用时空非度量性描述引力的广义相对论的对称远平行等价物 （STEGR）。在本文中，我们完成了非相对论引力的几何三位一体，方法是 （a） 取 STEGR 的非相对论极限来确定其非相对论类似物，以及 （b） 证明这种非度量理论等同于牛顿-卡坦理论及其遥平行等价物，即基于曲率和扭转的非相对论理论，它们都是经典牛顿引力的几何版本。