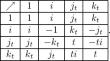
In this paper we describe the rise of global operators in the scaled quaternionic case, an important extension from the quaternionic case to the family of scaled hypercomplex numbers \(\mathbb {H}_t,\, t\in \mathbb {R}^*\), of which the \(\mathbb {H}_{-1}=\mathbb {H}\) is the space of quaternions and \(\mathbb {H}_{1}\) is the space of split quaternions. We also describe the scaled Fueter-type variables associated to these operators, developing a coherent theory in this field. We use these types of variables to build different types of function spaces on \(\mathbb {H}_t\). Counterparts of the Hardy space and of the Arveson space are also introduced and studied in the present setting. The two different adjoints in the scaled hypercomplex numbers lead to two parallel cases in each instance. Finally we introduce and study the notion of rational function.

在本文中，我们描述了缩放四元数情况下全局运算符的兴起，这是从四元数情况到缩放超复数 \（\mathbb {H}_t，\， t\in \mathbb {R}^*\） 族的重要扩展，其中 \（\mathbb {H}_{-1}=\mathbb {H}\） 是四元数的空间，\（\mathbb {H}_{1}\） 是分裂四元数的空间。我们还描述了与这些算子相关的缩放 Fueter 类型变量，在该领域发展了一个连贯的理论。我们使用这些类型的变量在 \（\mathbb {H}_t\） 上构建不同类型的函数空间。在当前环境中，还介绍和研究了 Hardy 空间和 Arveson 空间的对应物。缩放后的超复数中的两个不同的伴随导致每个实例中有两个平行的情况。最后，我们介绍和研究了有理函数的概念。