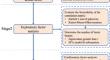
Students’ success in physics problem-solving extends beyond conceptual knowledge of physics, relying significantly on their mathematics skills. Understanding the specific contributions of different mathematics skills to physics problem-solving can offer valuable insights for enhancing physics education. Yet such studies are rare, particularly at the high school level. This study addresses the underexplored area of this topic in secondary education by investigating the associations between physics problem-solving performance using a robust methodological framework. We applied exploratory factor analysis (EFA) to identify latent sub-mathmetics skills relevant to physics problem-solving and employed structural equation modeling (SEM) to examine the causal impact of these skills on students’ performance in physics. The study analyzed data from a municipal-wide assessment involving 1,878 grade 12 students in Southern China. The results demonstrate that mathematics skills impacting high school students’ physics problem-solving performance can be categorized into two sub skills, algebraic skills and geometric skills. It also indicates that algebraic skills have a stronger direct effect on physics problem-solving performance compared to geometric skills in high school setting. These findings suggest that integrating focused algebraic training within physics education can significantly improve student outcomes in STEM fields. We recommend that educators design curricula and instructional strategies that emphasize the development of algebraic skills necessary for solving complex physics problems. Additionally, these findings have important implications for policymakers, who should consider integrating targeted mathematics training within physics curricula to foster interdisciplinary learning and better prepare students for challenges in STEM education.

学生解决物理问题的成功超出了物理概念知识的范围，很大程度上依赖于他们的数学技能。了解不同数学技能对解决物理问题的具体贡献可以为加强物理教育提供宝贵的见解。然而这样的研究很少见，尤其是在高中阶段。本研究通过使用强大的方法框架调查物理问题解决能力之间的关联，解决了中学教育中该主题尚未充分探索的领域。我们应用探索性因素分析（EFA）来识别与解决物理问题相关的潜在子数学技能，并采用结构方程模型（SEM）来检查这些技能对学生物理成绩的因果影响。该研究分析了一项涉及华南地区 1,878 名 12 年级学生的全市评估数据。结果表明，影响高中生物理问题解决能力的数学技能可以分为两个子技能：代数技能和几何技能。它还表明，与高中环境中的几何技能相比，代数技能对物理问题解决能力的直接影响更大。这些发现表明，将重点代数训练融入物理教育中可以显着提高学生在 STEM 领域的成绩。我们建议教育工作者设计课程和教学策略，强调解决复杂物理问题所需的代数技能的发展。 此外，这些发现对政策制定者具有重要意义，政策制定者应考虑将有针对性的数学培训纳入物理课程，以促进跨学科学习，让学生更好地应对 STEM 教育的挑战。