当前位置:
X-MOL 学术
›
J. Chem. Theory Comput.
›
论文详情
Our official English website, www.x-mol.net, welcomes your
feedback! (Note: you will need to create a separate account there.)
Spectral Map for Slow Collective Variables, Markovian Dynamics, and Transition State Ensembles
Journal of Chemical Theory and Computation ( IF 5.7 ) Pub Date : 2024-09-12 , DOI: 10.1021/acs.jctc.4c00428 Jakub Rydzewski 1
Journal of Chemical Theory and Computation ( IF 5.7 ) Pub Date : 2024-09-12 , DOI: 10.1021/acs.jctc.4c00428 Jakub Rydzewski 1
Affiliation
|
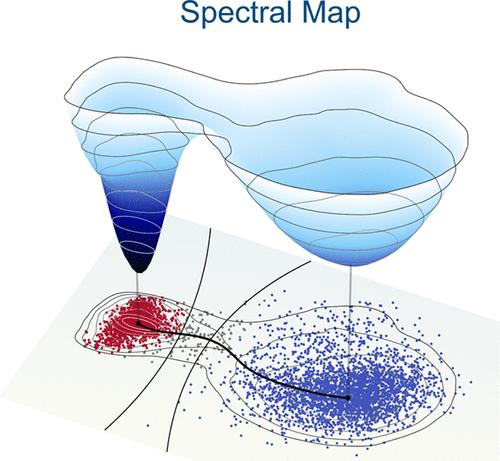
Understanding the behavior of complex molecular systems is a fundamental problem in physical chemistry. To describe the long-time dynamics of such systems, which is responsible for their most informative characteristics, we can identify a few slow collective variables (CVs) while treating the remaining fast variables as thermal noise. This enables us to simplify the dynamics and treat it as diffusion in a free-energy landscape spanned by slow CVs, effectively rendering the dynamics Markovian. Our recent statistical learning technique, spectral map [Rydzewski, J. J. Phys. Chem. Lett. 2023, 14(22), 5216–5220], explores this strategy to learn slow CVs by maximizing a spectral gap of a transition matrix. In this work, we introduce several advancements into our framework, using a high-dimensional reversible folding process of a protein as an example. We implement an algorithm for coarse-graining Markov transition matrices to partition the reduced space of slow CVs kinetically and use it to define a transition state ensemble. We show that slow CVs learned by spectral map closely approach the Markovian limit for an overdamped diffusion. We demonstrate that coordinate-dependent diffusion coefficients only slightly affect the constructed free-energy landscapes. Finally, we present how spectral maps can be used to quantify the importance of features and compare slow CVs with structural descriptors commonly used in protein folding. Overall, we demonstrate that a single slow CV learned by spectral map can be used as a physical reaction coordinate to capture essential characteristics of protein folding.
中文翻译:

慢集体变量、马尔可夫动力学和过渡态系综的谱图
了解复杂分子系统的行为是物理化学中的一个基本问题。为了描述此类系统的长期动态(这决定了其最具信息量的特征),我们可以识别一些慢速集体变量(CV),同时将剩余的快速变量视为热噪声。这使我们能够简化动力学并将其视为由慢速 CV 跨越的自由能景观中的扩散,从而有效地呈现动力学马尔可夫。我们最近的统计学习技术,光谱图 [Rydzewski, J. J. Phys.化学。莱特。 2023 , 14 (22), 5216–5220],探索了这种通过最大化转移矩阵的谱间隙来学习慢速 CV 的策略。在这项工作中,我们以蛋白质的高维可逆折叠过程为例,在我们的框架中引入了一些进步。我们实现了一种粗粒度马尔可夫转移矩阵算法,以动力学方式划分慢速 CV 的缩减空间,并用它来定义过渡状态系综。我们表明,通过谱图学习到的慢速 CV 非常接近过阻尼扩散的马尔可夫极限。我们证明,坐标相关的扩散系数仅对构建的自由能景观产生轻微影响。最后,我们介绍了如何使用光谱图来量化特征的重要性,并将慢速 CV 与蛋白质折叠中常用的结构描述符进行比较。总的来说,我们证明了通过光谱图学习的单个慢速 CV 可以用作物理反应坐标来捕获蛋白质折叠的基本特征。
更新日期:2024-09-12
中文翻译:

慢集体变量、马尔可夫动力学和过渡态系综的谱图
了解复杂分子系统的行为是物理化学中的一个基本问题。为了描述此类系统的长期动态(这决定了其最具信息量的特征),我们可以识别一些慢速集体变量(CV),同时将剩余的快速变量视为热噪声。这使我们能够简化动力学并将其视为由慢速 CV 跨越的自由能景观中的扩散,从而有效地呈现动力学马尔可夫。我们最近的统计学习技术,光谱图 [Rydzewski, J. J. Phys.化学。莱特。 2023 , 14 (22), 5216–5220],探索了这种通过最大化转移矩阵的谱间隙来学习慢速 CV 的策略。在这项工作中,我们以蛋白质的高维可逆折叠过程为例,在我们的框架中引入了一些进步。我们实现了一种粗粒度马尔可夫转移矩阵算法,以动力学方式划分慢速 CV 的缩减空间,并用它来定义过渡状态系综。我们表明,通过谱图学习到的慢速 CV 非常接近过阻尼扩散的马尔可夫极限。我们证明,坐标相关的扩散系数仅对构建的自由能景观产生轻微影响。最后,我们介绍了如何使用光谱图来量化特征的重要性,并将慢速 CV 与蛋白质折叠中常用的结构描述符进行比较。总的来说,我们证明了通过光谱图学习的单个慢速 CV 可以用作物理反应坐标来捕获蛋白质折叠的基本特征。































 京公网安备 11010802027423号
京公网安备 11010802027423号