Bridging Microscopic Dynamics and Hydraulic Permeability in Mechanically-Deformed Nanoporous Materials,ACS Nano

当前位置： X-MOL 学术 › ACS Nano › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

Bridging Microscopic Dynamics and Hydraulic Permeability in Mechanically-Deformed Nanoporous Materials
ACS Nano ( IF 15.8 ) Pub Date : 2024-09-10 , DOI: 10.1021/acsnano.4c04190
Alexander Schlaich _{1,

2,

3} , Matthieu Vandamme ₄ , Marie Plazanet ₃ , Benoit Coasne _{3,

5}

Affiliation

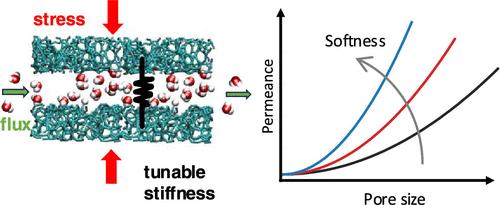
In the field of nanoconfined fluids, there are striking examples of deformation/transport coupling in which mechanical solicitation of the confining solid and dynamics of the confined fluid impact each other. While this intriguing behavior can be harnessed for applications (e.g., energy storage, phase separation, catalysis), the underlying mechanisms remain to be understood. Here, using molecular simulations, we investigate fluid flow in deformable nanoporous materials subjected to external mechanical stresses. We show that the pore mechanical properties significantly affect fluid flow as they lead to significant pore deformations and different fluid organization at the solid surface. Despite such mechanical effects, we show that the fluid thermodynamic properties (i.e., adsorption) can be linked consistently to Darcy’s law for the permeability by invoking a pore size definition based on the concept of Gibbs’ dividing surface. In particular, regardless of the solid stiffness and applied external stress, all data can be rationalized by accounting for the fluid viscosity and slippage at the solid surface (independently of a specific pore size definition). Using such a formalism, we establish that the intimate relation─derived using the linear response theory─between collective diffusivity and hydraulic permeability remains valid. This allows linking consistently microscopic dynamics experiments and macroscopic permeability experiments on fluid flow in deformable nanoporous materials.

中文翻译：

桥接机械变形纳米多孔材料的微观动力学和水力渗透率

在纳米约束流体领域，存在变形/输运耦合的惊人例子，其中约束固体的机械激发和约束流体的动力学相互影响。虽然这种有趣的行为可以用于应用（例如能量存储、相分离、催化），但其潜在机制仍有待理解。在这里，我们使用分子模拟研究了受到外部机械应力作用的可变形纳米多孔材料中的流体流动。我们表明，孔隙机械特性显着影响流体流动，因为它们会导致固体表面显着的孔隙变形和不同的流体组织。尽管存在这些机械效应，我们表明，通过调用基于吉布斯分割面概念的孔径定义，流体热力学性质（即吸附）可以与渗透率的达西定律一致地联系起来。特别是，无论固体刚度和施加的外部应力如何，所有数据都可以通过考虑固体表面的流体粘度和滑移（独立于特定的孔径定义）来合理化。利用这种形式主义，我们确定了集体扩散率和水力渗透率之间的密切关系（使用线性响应理论推导得出）仍然有效。这允许将可变形纳米多孔材料中的流体流动的微观动力学实验和宏观渗透性实验一致地联系起来。

更新日期：2024-09-10

点击分享查看原文

点击收藏

公开下载

阅读更多本刊新发论文本刊介绍/投稿指南