Grand Canonical Ensemble Approaches in CP2K for Modeling Electrochemistry at Constant Electrode Potentials,Journal of Chemical Theory and Computation

当前位置： X-MOL 学术 › J. Chem. Theory Comput. › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

Grand Canonical Ensemble Approaches in CP2K for Modeling Electrochemistry at Constant Electrode Potentials
Journal of Chemical Theory and Computation ( IF 5.7 ) Pub Date : 2024-09-06 , DOI: 10.1021/acs.jctc.4c00671
Ziwei Chai ₁ , Sandra Luber ₁

Affiliation

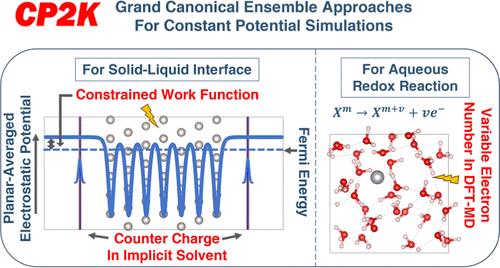
In electrochemical experiments, the number of electrons of the electrode immersed in the electrolyte is usually variable. Additionally, the numbers of adsorbed substances on the surface of the electrode, the solvent molecules, and counter charge ions in the near-surface region can also vary. Treating electrochemical solid–liquid interfaces with the typical fixed electron number density functional theory (DFT) approach tends to be a challenge. This can be addressed by using grand canonical ensemble approaches. We present the implementation of two grand canonical ensemble approaches in the open-source computational chemistry software CP2K that go beyond the existing canonical ensemble paradigm. The first approach is based on implicit solvent models and explicit atomistic solute (electrode with/without adsorbed species) models, and includes two recent developments: (a) grand canonical self-consistent field (GC-SCF) method (J. Chem. Phys. 2017, 146, 114104) allowing the electron number of the system to fluctuate naturally and accordingly with the experimental electrode potential, (b) planar counter charge (J. Chem. Phys. 2019, 150, 041722, Phys. Rev. B 2003, 68, 245416) salt model completely screening the net charge of the electrode model. In contrast with previous studies, in our implementation, the work function (WF) (absolute electrode potential if the potential drop at the electrolyte–vacuum interface is omitted) is the constrained quantity during an SCF optimization instead of the Fermi energy. The chemical potential of electrons (negative WF) is a natural variable of the grand potential in the GC ensemble of electronic states, and this method can easily achieve stable SCF convergence and obtain an electronic structure that precisely corresponds to a user-specified WF. The second approach referred to as the GC DFT molecular dynamics (DFT-MD) simulation scheme (Phys. Rev. Lett. 2002, 88, 213002, J. Chem. Phys. 2005, 122, 234505, J. Am. Chem. Soc. 2004, 126 (12), 3928–3938) is based on fully explicit modeling the solvent molecules and the ions and is used to calculate the electron chemical potential corresponding to an equilibrium electrochemical half-reaction (M^(n+m)+ + ne^– ⇌ M^m+) which involves DFT-MD, by allowing the number of electrons to vary during the DFT-MD simulation process. This opens the way for forefront electrochemical calculations in CP2K for a broad range of systems.

中文翻译：

CP2K 中用于模拟恒定电极电势电化学的大正则系综方法

在电化学实验中，浸入电解质中的电极的电子数量通常是可变的。此外，电极表面吸附物质、溶剂分子和近表面区域反电荷离子的数量也会变化。使用典型的固定电子数密度泛函理论（DFT）方法处理电化学固液界面往往是一个挑战。这可以通过使用大规范集成方法来解决。我们在开源计算化学软件 CP2K 中提出了两种大规范系综方法的实现，这些方法超越了现有的规范系综范式。第一种方法基于隐式溶剂模型和显式原子溶质（有/无吸附物质的电极）模型，并包括两项最新进展：（a）大正则自洽场（GC-SCF）方法（ J. Chem. Phys） . 2017, 146, 114104) 允许系统的电子数随实验电极电势自然波动，(b) 平面反电荷 ( J. Chem. Phys. 2019, 150, 041722, Phys. Rev. B 2003 , 68, 245416) 盐模型完全筛选了电极模型的净电荷。与之前的研究相比，在我们的实现中，功函数（WF）（如果省略电解质-真空界面处的电势降，则为绝对电极电势）是SCF优化期间的约束量，而不是费米能量。电子的化学势（负WF）是GC电子态系综中大势的自然变量，该方法可以轻松实现稳定的SCF收敛并获得与用户指定的WF精确对应的电子结构。第二种方法称为 GC DFT 分子动力学 (DFT-MD) 模拟方案 ( Phys. Rev. Lett. 2002, 88, 213002, J. Chem. Phys. 2005, 122, 234505, J. Am. Chem. Soc 2004 , 126 (12) 3928–3938) 基于溶剂分子和离子的完全显式建模，用于计算对应于平衡电化学半反应 ( M ^{( n + m )+} + ne 的电子化学势。 ^– ⇌ M ^{m +} ) 涉及 DFT-MD，通过允许电子数量在 DFT-MD 模拟过程中变化。这为 CP2K 中适用于各种系统的前沿电化学计算开辟了道路。

更新日期：2024-09-06

点击分享查看原文

点击收藏

阅读更多本刊新发论文本刊介绍/投稿指南