Reaction Networks Resemble Low-Dimensional Regular Lattices,Journal of Chemical Theory and Computation

当前位置： X-MOL 学术 › J. Chem. Theory Comput. › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

Reaction Networks Resemble Low-Dimensional Regular Lattices
Journal of Chemical Theory and Computation ( IF 5.7 ) Pub Date : 2024-09-05 , DOI: 10.1021/acs.jctc.4c00810
Miko M Stulajter _{1,

2} , Dmitrij Rappoport ₁

Affiliation

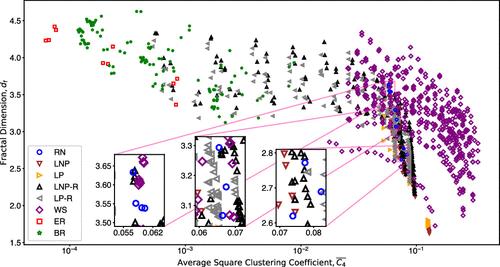
The computational exploration, manipulation, and design of complex chemical reactions face fundamental challenges related to the high-dimensional nature of potential energy surfaces (PESs) that govern reactivity. Accurately modeling complex reactions is crucial for understanding the chemical processes involved in, for example, organocatalysis, autocatalytic cycles, and one-pot molecular assembly. Our prior research demonstrated that discretizing PESs using heuristics based on bond breaking and bond formation produces a reaction network representation with a low-dimensional structure (metric space). We now find that these stoichiometry-preserving reaction networks possess additional, though approximate, structure and resemble low-dimensional regular lattices with a small amount of random edge rewiring. The heuristics-based discretization thus generates a nonlinear dimensionality reduction by a factor of 10 with an a posteriori error measure (probability of random rewiring). The structure becomes evident through a comparative analysis of CHNO reaction networks of varying stoichiometries against a panel of size-matched generative network models, taking into account their local, metric, and global properties. The generative models include random networks (Erdős−Rényi and bipartite random networks), regular lattices (periodic and nonperiodic), and network models with a tunable level of “randomness” (Watts–Strogatz graphs and regular lattices with random rewiring). The CHNO networks are simultaneously closely matched in all these properties by 3–4-dimensional regular lattices with 10% or less of edges randomly rewired. The effective dimensionality reduction is found to be independent of the system size, stoichiometry, and ruleset, suggesting that search and sampling algorithms for PESs of complex chemical reactions can be effectively leveraged.

中文翻译：

反应网络类似于低维规则格子

复杂化学反应的计算探索、操作和设计面临着与控制反应性的势能表面 (PES) 的高维性质相关的基本挑战。准确模拟复杂反应对于理解有机催化、自催化循环和一锅分子组装等涉及的化学过程至关重要。我们之前的研究表明，使用基于键断裂和键形成的启发式离散化 PES 会产生具有低维结构（度量空间）的反应网络表示。我们现在发现这些保持化学计量的反应网络具有额外的、虽然近似的结构，并且类似于具有少量随机边缘重新布线的低维规则晶格。因此，基于启发式的离散化可以通过后验误差测量（随机重新布线的概率）将非线性维度降低 10 倍。通过对不同化学计量的 CHNO 反应网络与一组尺寸匹配的生成网络模型进行比较分析，考虑到它们的局部、度量和全局特性，该结构变得显而易见。生成模型包括随机网络（Erdős−Rényi 和二分随机网络）、规则格子（周期性和非周期性）以及具有可调节“随机性”水平的网络模型（Watts-Strogatz 图和具有随机重新布线的规则格子）。 CHNO 网络在所有这些特性上同时通过 3-4 维规则晶格紧密匹配，其中 10% 或更少的边缘随机重新连接。研究发现，有效的降维与系统尺寸、化学计量和规则集无关，这表明可以有效地利用复杂化学反应的 PES 的搜索和采样算法。

更新日期：2024-09-05

点击分享查看原文

点击收藏

阅读更多本刊新发论文本刊介绍/投稿指南