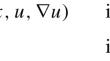
In this paper, the existence of weak solutions to some Dirichlet problems with fractional competing operators and distributional Riesz fractional gradient is investigated. Due to the nature of driving operators, the most known techniques, basically based on ellipticity and monotonicity, are no longer applicable. Generalized solutions (in a suitable sense) are obtained via an approximation procedure and a corollary of the Brouwer fixed point theorem.

中文翻译：

---

分数竞争算子和分数对流的狄利克雷问题

本文研究了一些具有分数竞争算子和分布 Riesz 分数梯度的 Dirichlet 问题的弱解的存在性。由于驾驶算子的性质，大多数已知的技术（基本上基于椭圆性和单调性）不再适用。广义解（在适当的意义上）是通过近似过程和布劳威尔不动点定理的推论获得的。