van der Waals Radii of Free and Bonded Atoms from Hydrogen (Z = 1) to Oganesson (Z = 118),Journal of Chemical Theory and Computation

当前位置： X-MOL 学术 › J. Chem. Theory Comput. › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

van der Waals Radii of Free and Bonded Atoms from Hydrogen (Z = 1) to Oganesson (Z = 118)
Journal of Chemical Theory and Computation ( IF 5.7 ) Pub Date : 2024-08-29 , DOI: 10.1021/acs.jctc.4c00784
Jorge Charry ₁ , Alexandre Tkatchenko ₁

Affiliation

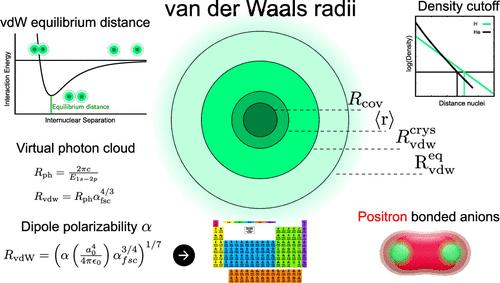
Reliable numerical values of van der Waals (vdW) radii are required for constructing empirical force fields, vdW-inclusive density functional, and quantum-chemical methods, as well as for implicit solvent models. However, multiple definitions exist for vdW radii, involving either equilibrium or the closest contact distances between free or bonded atoms within molecules or crystals. For the paradigmatic case of the hydrogen atom, its reported vdW radius fluctuates between 2.15 and 3.70 Bohr depending on the definition, leading to a high uncertainty in calculations and different conceptual interpretations of noncovalent interactions. In this work, we systematically review different definitions and methodologies to establish the free and bonded vdW radii for hydrogen, based on equilibrium vdW distances in noncovalently bonded molecules, enveloping electron density cutoffs, noncovalent positron bonds in hydrogen anion dimer, vacuum virtual photon cloud caused by the hydrogen atom, and atomic dipole polarizability. By doing so, we show that the vdW radius of the free hydrogen atom is 3.16 ± 0.06 Bohr. By employing the most general and elegant definition of atomic vdW radius as a function of the atomic polarizability, we tabulate consistent values of vdW radii for all atoms in the periodic table up to Z = 118.

中文翻译：

从氢 (Z = 1) 到 Oganesson (Z = 118) 的自由原子和键合原子的范德华半径

构建经验力场、包含 vdW 的密度泛函和量子化学方法以及隐式溶剂模型需要可靠的范德华 (vdW) 半径数值。然而，vdW 半径存在多种定义，涉及分子或晶体内自由或键合原子之间的平衡或最近接触距离。对于氢原子的典型情况，其报道的 vdW 半径根据定义在 2.15 和 3.70 玻尔之间波动，导致计算的高度不确定性和非共价相互作用的不同概念解释。在这项工作中，我们系统地回顾了不同的定义和方法，以建立氢的自由和键合 vdW 半径，基于非共价键分子中的平衡 vdW 距离、包络电子密度截止、氢阴离子二聚体中的非共价正电子键、真空虚拟光子云引起的由氢原子和原子偶极子极化率决定。通过这样做，我们表明自由氢原子的 vdW 半径为 3.16 ± 0.06 Bohr。通过采用原子 vdW 半径最通用和最优雅的定义作为原子极化率的函数，我们列出了元素周期表中直至Z = 118 的所有原子的一致 vdW 半径值。

更新日期：2024-08-29

点击分享查看原文

点击收藏

公开下载

阅读更多本刊新发论文本刊介绍/投稿指南