Convergence Analysis of the Stochastic Resolution of Identity: Comparing Hutchinson to Hutch++ for the Second-Order Green’s Function,Journal of Chemical Theory and Computation

当前位置： X-MOL 学术 › J. Chem. Theory Comput. › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

Convergence Analysis of the Stochastic Resolution of Identity: Comparing Hutchinson to Hutch++ for the Second-Order Green’s Function
Journal of Chemical Theory and Computation ( IF 5.7 ) Pub Date : 2024-08-27 , DOI: 10.1021/acs.jctc.4c00862
Leopoldo Mejía _{1,

2} , Sandeep Sharma ₃ , Roi Baer ₄ , Garnet Kin-Lic Chan ₅ , Eran Rabani _{1,

2,

6}

Affiliation

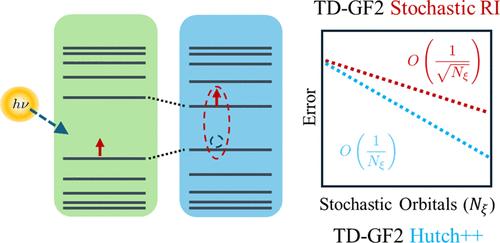
Stochastic orbital techniques offer reduced computational scaling and memory requirements to describe ground and excited states at the cost of introducing controlled statistical errors. Such techniques often rely on two basic operations, stochastic trace estimation and stochastic resolution of identity, both of which lead to statistical errors that scale with the number of stochastic realizations (N_ξ) as

\sqrt{N_{ξ}^{- 1}}

$\sqrt{N_{ξ}^{- 1}}$ . Reducing the statistical errors without significantly increasing N_ξ has been challenging and is central to the development of efficient and accurate stochastic algorithms. In this work, we build upon recent progress made to improve stochastic trace estimation based on the ubiquitous Hutchinson’s algorithm and propose a two-step approach for the stochastic resolution of identity, in the spirit of the Hutch++ method. Our approach is based on employing a randomized low-rank approximation followed by a residual calculation, resulting in statistical errors that scale much better than

\sqrt{N_{ξ}^{- 1}}

$\sqrt{N_{ξ}^{- 1}}$ . We implement the approach within the second-order Born approximation for the self-energy in the computation of neutral excitations and discuss three different low-rank approximations for the two-body Coulomb integrals. Tests on a series of hydrogen dimer chains with varying lengths demonstrate that the Hutch++-like approximations are computationally more efficient than both deterministic and purely stochastic (Hutchinson) approaches for low error thresholds and intermediate system sizes. Notably, for arbitrarily large systems, the Hutchinson-like approximation outperforms both deterministic and Hutch++-like methods.

中文翻译：

恒等式随机分解的收敛性分析：二阶格林函数的 Hutchinson 与 Hutch++ 的比较

随机轨道技术减少了描述基态和激发态的计算规模和内存需求，但代价是引入受控统计误差。此类技术通常依赖于两个基本操作，即随机迹估计和身份的随机解析，这两者都会导致统计误差，该误差随着随机实现的数量 ( N _xi ) 的变化而变化，如下所示：

\sqrt{N_{ξ}^{- 1}}

$\sqrt{N_{ξ}^{- 1}}$
。在不显着增加N _{ϵ 的}情况下减少统计误差一直是一项挑战，也是开发高效、准确的随机算法的核心。在这项工作中，我们以最近在改进基于普遍存在的 Hutchinson 算法的随机迹估计方面取得的进展为基础，并本着 Hutch++ 方法的精神，提出了一种用于身份随机解析的两步方法。我们的方法基于采用随机低秩近似，然后进行残差计算，导致统计误差比

\sqrt{N_{ξ}^{- 1}}

$\sqrt{N_{ξ}^{- 1}}$
。我们在中性激励计算中的自能二阶玻恩近似中实现了该方法，并讨论了双体库仑积分的三种不同的低阶近似。对一系列不同长度的氢二聚体链的测试表明，对于低误差阈值和中等系统大小，类似 Hutch++ 的近似方法在计算上比确定性方法和纯随机 (Hutchinson) 方法更有效。值得注意的是，对于任意大的系统，类 Hutchinson 近似方法的性能优于确定性方法和类 Hutch++ 方法。

更新日期：2024-08-27

点击分享查看原文

点击收藏

公开下载

阅读更多本刊新发论文本刊介绍/投稿指南