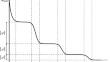
Gradient-based learning in multi-layer neural networks displays a number of striking features. In particular, the decrease rate of empirical risk is non-monotone even after averaging over large batches. Long plateaus in which one observes barely any progress alternate with intervals of rapid decrease. These successive phases of learning often take place on very different time scales. Finally, models learnt in an early phase are typically ‘simpler’ or ‘easier to learn’ although in a way that is difficult to formalize. Although theoretical explanations of these phenomena have been put forward, each of them captures at best certain specific regimes. In this paper, we study the gradient flow dynamics of a wide two-layer neural network in high-dimension, when data are distributed according to a single-index model (i.e., the target function depends on a one-dimensional projection of the covariates). Based on a mixture of new rigorous results, non-rigorous mathematical derivations, and numerical simulations, we propose a scenario for the learning dynamics in this setting. In particular, the proposed evolution exhibits separation of timescales and intermittency. These behaviors arise naturally because the population gradient flow can be recast as a singularly perturbed dynamical system.

多层神经网络中基于梯度的学习显示出许多引人注目的特征。特别是，即使在大批量平均后，经验风险的下降率也是非单调的。人们几乎观察不到任何进展的长期平稳期与快速下降的间歇期交替出现。这些连续的学习阶段通常发生在非常不同的时间范围内。最后，早期学习的模型通常“更简单”或“更容易学习”，尽管其方式很难形式化。尽管已经提出了对这些现象的理论解释，但它们中的每一个都最多描述了某些特定的情况。在本文中，我们研究了高维宽两层神经网络的梯度流动力学，当数据根据单指数模型分布时（即目标函数取决于协变量的一维投影） ）。基于新的严格结果、非严格数学推导和数值模拟的结合，我们提出了这种情况下的学习动态场景。特别是，所提出的演化表现出时间尺度的分离和间歇性。这些行为自然会出现，因为群体梯度流可以被重新塑造为一个奇异扰动的动力系统。