当前位置:
X-MOL 学术
›
Macromolecules
›
论文详情
Our official English website, www.x-mol.net, welcomes your
feedback! (Note: you will need to create a separate account there.)
Correction to “Surface Segregation in Athermal Polymer Blends Due to Conformational Asymmetry”
Macromolecules ( IF 5.1 ) Pub Date : 2024-08-19 , DOI: 10.1021/acs.macromol.4c01641 Russell K. W. Spencer , Mark W. Matsen
Macromolecules ( IF 5.1 ) Pub Date : 2024-08-19 , DOI: 10.1021/acs.macromol.4c01641 Russell K. W. Spencer , Mark W. Matsen
|
The Monte Carlo code used for our paper (1) contained an error in the calculation of the bending energy of the stiff polymers for the crankshaft move. We have now recalculated all of the data published therein. The main conclusions have not changed; however, some minor differences should be pointed out. The primary effect of correcting the error is to increase the stiffness of the stiff polymers such that similar behavior is now achieved with smaller values of κ. For example, the bulk isotropic–nematic transition in
中文翻译:

对“由于构象不对称导致的非热聚合物共混物中的表面偏析”的修正
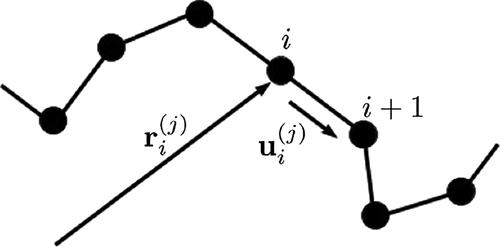
我们的论文 (1) 使用的蒙特卡罗代码在计算曲轴移动的刚性聚合物的弯曲能时存在错误。我们现在重新计算了其中发布的所有数据。主要结论没有改变;然而,应该指出一些细微的差别。修正误差的主要作用是增加刚性聚合物的刚度,这样现在可以用较小的 κ 值实现类似的行为。例如,参考文献 (1) 图 2 中的体各向同性向列相转变在质量上保持相似,但从 κ ≈ 6.0 k B T转变为 κ ≈ 3.5 k B T 。此外,与参考文献 (1) 中的图 5a、7a 和 12a 相比,硬壁 ( z = 0) 旁边的刚性聚合物数量有所增加。这使得结果与我们随后的出版物 (2) 更加一致,该出版物使用切球模型研究了相同的问题。通用隔离配置文件仍然有效。最后,对于渐变界面,聚合物表面的本体侧不再存在向列区域(参见参考文献(1)的图10)。最重要的特征仍然存在:表面附近的双轴有序和表面上的向列有序,并且刚性聚合物末端突出。尽管定性行为保持大致相同,但参考文献(1)中的所有结果都受到误差的影响,因此我们提供了一组完整的修订后的数据,如下所示。图 1. 显示第 j个聚合物的一部分的图示。 第i个单体的位置由矢量r ( j )表示,其与第( i +1)个单体的键合方向由单位矢量u ( j )表示。图 2. 刚性聚合物的向列序参数S与其弯曲模量 κ 的函数关系。虚线和实线分别用于用 κ = 0 和 5 k B T的平衡配置初始化的模拟。插图显示了刚性(红色)和柔性(蓝色)聚合物在均匀各向同性状态和两种具有弱有序和强有序的分层各向同性向列态的配置。主要变化是相变现在发生在 κ ≈ 3.5 k B T附近,而不是 κ ≈ 6.0 k B T 。图 3. 本体各向同性相中刚性聚合物(实线)和柔性聚合物(虚线)的平均端到端长度R 0与刚性聚合物弯曲模量 κ 的函数关系。图 4. 模拟盒中柔性聚合物(蓝色)和 κ = 3.3 k B T的刚性聚合物(红色)的平衡配置,该模拟盒在x和y方向具有周期性边界,在z方向两端具有硬壁。图 5. 硬质聚合物的整体平均浓度 ψ s ( z )(实线)和柔性聚合物 ψ f ( z )(虚线),紧邻z = 0 处的硬墙,评估 (a) κ = 1.6 k B T ,(b) κ = 3 k B T ,(c) κ = 3.3 k B T 。虚线表示平均浓度 [ψ s ( z ) + ψ f ( z )]/2,对应于无偏析,图 (a) 中的黑色曲线绘制了拟合 ψ f ( z ) = 0.0558 F ρ ( Z )+0.397。请注意,κ 的值已从参考文献 (1) 的值中降低,以说明刚性聚合物的刚度增加。对于 κ 的最低值,第一层 ( z = 0) 现在富含刚性链,而之前则富含柔性链。此外, z > 0 的拟合现在更加精确。图 6. 针对 (a) κ = 1.6 k B T 、(b) κ 评估的刚性聚合物的向列有序参数S ( z )(实线)和双轴有序参数P ( z )(虚线) = 3 k B T ,并且 (c) κ = 3.3 k B T 。在所有情况下,向列指向矢n均平行于壁。 请注意,κ 的值已从参考文献 (1) 的值中降低,以说明刚性聚合物的刚度增加。对于具有双轴表面顺序的两种情况, P ( z ) 现在在靠近壁的正z处呈现峰值。图 7. (a) 与表面相邻的第一 ( z = 0) 和第二 ( z = d ) 平面中刚性聚合物的过量浓度, ψ ex ( z ),(b) 刚性链的积分过量, Γ ex ,(c) 邻近表面的取向顺序参数S (0) 和P (0),绘制为刚性链弯曲模量 κ 的函数。现在,第一层往往富含刚性链,直到第二层才会出现柔性链显着过剩。此外,表面转变现在发生在 κ ≈ 2.8 k B T而不是 κ ≈ 3.8 k B T处。图 8.来自模拟盒的柔性聚合物(蓝色)和 κ = 3 k B T的刚性聚合物(红色)的示例配置,在x和y方向上具有周期性边界,在z方向两端具有软表面。图 9. 与图 5b 类似的图,但表面轮廓是渐变的,如虚线所示。顶部的间隔表示富含刚性聚合物的外部区域(即, ψ ex ( z ) > 0 )和富含柔性聚合物的内部区域(即 ψ ex ( z ) < 0 )。 请注意,κ 的值已从参考文献 (1) 的值中减小,以说明刚性聚合物的刚度增加。另请注意,负z处的刚性过剩比以前不那么明显。图 10. 与图 6b 类似的图,但表面轮廓是渐变的。向列指向矢n平行于表面,其中S ( z ) = P ( z )/3 且垂直于表面,其中S ( z ) > P ( z )/3 。请注意,κ 的值已从参考文献 (1) 的值中减小,以说明刚性聚合物的刚度增加。另请注意,仅当z < 0 时, n才会变得垂直。 图 11. 刚性聚合物的积分过量与其弯曲模量 κ(实线)的函数关系。虚线显示了图 9 中所示的外部和内部区域的贡献 Γ +和 Γ – ,其中 ψ ex ( z ) 分别为正和负。主要变化是Λ –现在单调递减,Λ +的贡献大大减少。图 12. 与图 5 类似的图,但壁电位关闭(即w ( z ) = 0)。 (a) 图中的黑色曲线表示拟合 ψ f ( z ) = 0.0965 F ρ ( Z ) + 0.3930。请注意,κ 的值已从参考文献 (1) 的值中降低,以说明刚性聚合物的刚度增加。此外,对于较小的 κ 值,壁上不再有明显过量的柔性链( z = 0)。 本文引用了另外 2 篇出版物。这篇文章尚未被其他出版物引用。
更新日期:2024-08-19
中文翻译:

对“由于构象不对称导致的非热聚合物共混物中的表面偏析”的修正
我们的论文 (1) 使用的蒙特卡罗代码在计算曲轴移动的刚性聚合物的弯曲能时存在错误。我们现在重新计算了其中发布的所有数据。主要结论没有改变;然而,应该指出一些细微的差别。修正误差的主要作用是增加刚性聚合物的刚度,这样现在可以用较小的 κ 值实现类似的行为。例如,参考文献 (1) 图 2 中的体各向同性向列相转变在质量上保持相似,但从 κ ≈ 6.0 k B T转变为 κ ≈ 3.5 k B T 。此外,与参考文献 (1) 中的图 5a、7a 和 12a 相比,硬壁 ( z = 0) 旁边的刚性聚合物数量有所增加。这使得结果与我们随后的出版物 (2) 更加一致,该出版物使用切球模型研究了相同的问题。通用隔离配置文件仍然有效。最后,对于渐变界面,聚合物表面的本体侧不再存在向列区域(参见参考文献(1)的图10)。最重要的特征仍然存在:表面附近的双轴有序和表面上的向列有序,并且刚性聚合物末端突出。尽管定性行为保持大致相同,但参考文献(1)中的所有结果都受到误差的影响,因此我们提供了一组完整的修订后的数据,如下所示。图 1. 显示第 j个聚合物的一部分的图示。 第i个单体的位置由矢量r ( j )表示,其与第( i +1)个单体的键合方向由单位矢量u ( j )表示。图 2. 刚性聚合物的向列序参数S与其弯曲模量 κ 的函数关系。虚线和实线分别用于用 κ = 0 和 5 k B T的平衡配置初始化的模拟。插图显示了刚性(红色)和柔性(蓝色)聚合物在均匀各向同性状态和两种具有弱有序和强有序的分层各向同性向列态的配置。主要变化是相变现在发生在 κ ≈ 3.5 k B T附近,而不是 κ ≈ 6.0 k B T 。图 3. 本体各向同性相中刚性聚合物(实线)和柔性聚合物(虚线)的平均端到端长度R 0与刚性聚合物弯曲模量 κ 的函数关系。图 4. 模拟盒中柔性聚合物(蓝色)和 κ = 3.3 k B T的刚性聚合物(红色)的平衡配置,该模拟盒在x和y方向具有周期性边界,在z方向两端具有硬壁。图 5. 硬质聚合物的整体平均浓度 ψ s ( z )(实线)和柔性聚合物 ψ f ( z )(虚线),紧邻z = 0 处的硬墙,评估 (a) κ = 1.6 k B T ,(b) κ = 3 k B T ,(c) κ = 3.3 k B T 。虚线表示平均浓度 [ψ s ( z ) + ψ f ( z )]/2,对应于无偏析,图 (a) 中的黑色曲线绘制了拟合 ψ f ( z ) = 0.0558 F ρ ( Z )+0.397。请注意,κ 的值已从参考文献 (1) 的值中降低,以说明刚性聚合物的刚度增加。对于 κ 的最低值,第一层 ( z = 0) 现在富含刚性链,而之前则富含柔性链。此外, z > 0 的拟合现在更加精确。图 6. 针对 (a) κ = 1.6 k B T 、(b) κ 评估的刚性聚合物的向列有序参数S ( z )(实线)和双轴有序参数P ( z )(虚线) = 3 k B T ,并且 (c) κ = 3.3 k B T 。在所有情况下,向列指向矢n均平行于壁。 请注意,κ 的值已从参考文献 (1) 的值中降低,以说明刚性聚合物的刚度增加。对于具有双轴表面顺序的两种情况, P ( z ) 现在在靠近壁的正z处呈现峰值。图 7. (a) 与表面相邻的第一 ( z = 0) 和第二 ( z = d ) 平面中刚性聚合物的过量浓度, ψ ex ( z ),(b) 刚性链的积分过量, Γ ex ,(c) 邻近表面的取向顺序参数S (0) 和P (0),绘制为刚性链弯曲模量 κ 的函数。现在,第一层往往富含刚性链,直到第二层才会出现柔性链显着过剩。此外,表面转变现在发生在 κ ≈ 2.8 k B T而不是 κ ≈ 3.8 k B T处。图 8.来自模拟盒的柔性聚合物(蓝色)和 κ = 3 k B T的刚性聚合物(红色)的示例配置,在x和y方向上具有周期性边界,在z方向两端具有软表面。图 9. 与图 5b 类似的图,但表面轮廓是渐变的,如虚线所示。顶部的间隔表示富含刚性聚合物的外部区域(即, ψ ex ( z ) > 0 )和富含柔性聚合物的内部区域(即 ψ ex ( z ) < 0 )。 请注意,κ 的值已从参考文献 (1) 的值中减小,以说明刚性聚合物的刚度增加。另请注意,负z处的刚性过剩比以前不那么明显。图 10. 与图 6b 类似的图,但表面轮廓是渐变的。向列指向矢n平行于表面,其中S ( z ) = P ( z )/3 且垂直于表面,其中S ( z ) > P ( z )/3 。请注意,κ 的值已从参考文献 (1) 的值中减小,以说明刚性聚合物的刚度增加。另请注意,仅当z < 0 时, n才会变得垂直。 图 11. 刚性聚合物的积分过量与其弯曲模量 κ(实线)的函数关系。虚线显示了图 9 中所示的外部和内部区域的贡献 Γ +和 Γ – ,其中 ψ ex ( z ) 分别为正和负。主要变化是Λ –现在单调递减,Λ +的贡献大大减少。图 12. 与图 5 类似的图,但壁电位关闭(即w ( z ) = 0)。 (a) 图中的黑色曲线表示拟合 ψ f ( z ) = 0.0965 F ρ ( Z ) + 0.3930。请注意,κ 的值已从参考文献 (1) 的值中降低,以说明刚性聚合物的刚度增加。此外,对于较小的 κ 值,壁上不再有明显过量的柔性链( z = 0)。 本文引用了另外 2 篇出版物。这篇文章尚未被其他出版物引用。

































 京公网安备 11010802027423号
京公网安备 11010802027423号