Renormalized Internally Contracted Multireference Coupled Cluster with Perturbative Triples,Journal of Chemical Theory and Computation

当前位置： X-MOL 学术 › J. Chem. Theory Comput. › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

Renormalized Internally Contracted Multireference Coupled Cluster with Perturbative Triples
Journal of Chemical Theory and Computation ( IF 5.7 ) Pub Date : 2024-08-19 , DOI: 10.1021/acs.jctc.4c00679
Robin Feldmann ₁ , Markus Reiher ₁

Affiliation

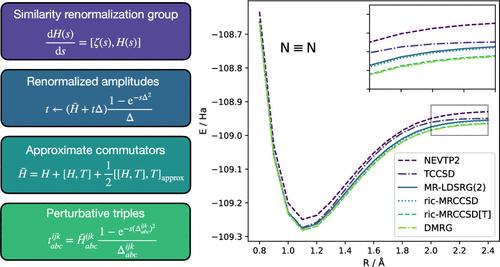
In this work, we combine the many-body formulation of the internally contracted multireference coupled cluster (ic-MRCC) method with Evangelista’s multireference formulation of the driven similarity renormalization group (DSRG). The DSRG method can be viewed as a unitary multireference coupled cluster theory, which renormalizes the amplitudes based on a flow equation approach to eliminate numerical instabilities. We extend this approach by demonstrating that the unitary flow equation approach can be adapted for nonunitary transformations, rationalizing the renormalization of ic-MRCC amplitudes. We denote the new approach, the renormalized ic-MRCC (ric-MRCC) method. To achieve high accuracy with a reasonable computational cost, we introduce a new approximation to the Baker–Campbell–Hausdorff expansion. We fully consider the linear commutator while approximating the quadratic commutator, for which we neglect specific contractions involving amplitudes with active indices. Moreover, we introduce approximate perturbative triples to obtain the ric-MRCCSD[T] method. We demonstrate the accuracy of our approaches in comparison to advanced multireference methods for the potential energy curves of H₈, F₂, H₂O, N₂, and Cr₂. Additionally, we show that ric-MRCCSD and ric-MRCSSD[T] match the accuracy of CCSD(T) for evaluating spectroscopic constants and of full configuration interaction energies for a set of small molecules.

中文翻译：

具有微扰三元组的重正化内收缩多参考耦合簇

在这项工作中，我们将内部收缩多参考耦合簇 (ic-MRCC) 方法的多体公式与 Evangelista 驱动相似性重正化群 (DSRG) 的多参考公式相结合。 DSRG 方法可以被视为酉多参考耦合聚类理论，它基于流动方程方法对振幅进行重新归一化，以消除数值不稳定性。我们通过证明酉流动方程方法可以适用于非酉变换，从而使 ic-MRCC 振幅的重整化合理化，从而扩展了这种方法。我们表示新方法，即重整化 ic-MRCC (ric-MRCC) 方法。为了以合理的计算成本实现高精度，我们引入了 Baker-Campbell-Hausdorff 展开式的新近似。我们在近似二次换向器时充分考虑线性换向器，为此我们忽略了涉及具有有效指数的幅度的特定收缩。此外，我们引入近似微扰三元组来获得ric-MRCCSD[T]方法。与 H ₈ 、F ₂ 、H ₂ O、N ₂和 Cr ₂势能曲线的先进多参考方法相比，我们证明了我们的方法的准确性。此外，我们还表明，ric-MRCCSD 和 ric-MRCSSD[T] 与 CCSD(T) 评估光谱常数和一组小分子的全构型相互作用能的准确性相匹配。

更新日期：2024-08-19

点击分享查看原文

点击收藏

公开下载

阅读更多本刊新发论文本刊介绍/投稿指南