Advanced Mathematical Model for the Transport of Aggregating Nanoparticles in Water Saturated Porous Media: Nonlinear Attachment and Particle Size-Dependent Dispersion,Water Resources Research

当前位置： X-MOL 学术 › Water Resour. Res. › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

Advanced Mathematical Model for the Transport of Aggregating Nanoparticles in Water Saturated Porous Media: Nonlinear Attachment and Particle Size-Dependent Dispersion
Water Resources Research ( IF 4.6 ) Pub Date : 2024-08-19 , DOI: 10.1029/2024wr037056
Vasileios E. Katzourakis ₁ , Constantinos V. Chrysikopoulos _{1,

2}

Affiliation

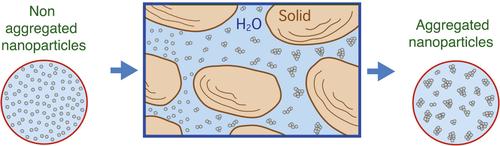
A conceptual mathematical model was developed to describe the migration of aggregating nanoparticles in water saturated, homogeneous porous media with one-dimensional uniform flow. Nanoparticles can be found suspended in the aqueous phase or attached reversibly and/or irreversibly onto the solid matrix. The Smoluchowski population balance equation (PBE) was used to model the process of particle aggregation and was coupled with the advection-dispersion-attachment equation to form a nonlinear transport model. Furthermore, an efficient and accurate solver for the PBE, and an iterative solver for the linear or nonlinear attachment equations were employed. The new numerical model was applied to nanoparticle transport experimental data available in the literature. Although, conventional transport models can be used to describe nanoparticle migration at low ionic strength conditions, such models might not be applicable for high ionic strength conditions, where aggregation becomes a dominant process. Aggregation is significantly affecting the transport characteristics of nanoparticles. Under high ionic strength conditions, the mass retention in the solid matrix of the porous medium increases, and a nonlinear particle attachment behavior may be observed. The proposed model performed remarkably well, successfully capturing numerous physical processes associated with nanoparticle transport, including particle-size-dependent dispersion. Ignoring the aggregation process and using conventional colloidal transport models to model nanoparticle transport may lead to erroneous results.

中文翻译：

水饱和多孔介质中聚集纳米粒子输运的高级数学模型：非线性附着和粒度依赖性分散

开发了一个概念数学模型来描述聚集纳米颗粒在水饱和、具有一维均匀流动的均匀多孔介质中的迁移。纳米颗粒可以悬浮在水相中或可逆和/或不可逆地附着在固体基质上。 Smoluchowski种群平衡方程（PBE）用于模拟颗粒聚集过程，并与平流-弥散-附着方程耦合形成非线性输运模型。此外，还采用了高效且准确的 PBE 求解器以及线性或非线性附着方程的迭代求解器。新的数值模型应用于文献中提供的纳米颗粒输运实验数据。尽管传统的传输模型可用于描述低离子强度条件下的纳米粒子迁移，但此类模型可能不适用于高离子强度条件，在高离子强度条件下，聚集成为主要过程。聚集显着影响纳米粒子的传输特性。在高离子强度条件下，多孔介质固体基质中的质量保留增加，并且可以观察到非线性颗粒附着行为。所提出的模型表现非常好，成功捕获了与纳米颗粒传输相关的许多物理过程，包括依赖于颗粒尺寸的分散。忽略聚集过程并使用传统的胶体传输模型来模拟纳米颗粒传输可能会导致错误的结果。

更新日期：2024-08-19

点击分享查看原文

点击收藏

公开下载

阅读更多本刊新发论文本刊介绍/投稿指南