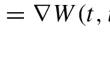
Consider the following fractional Hamiltonian system:

Here, \(_{t}D_{\infty }^{\alpha }\) and \(_{-\infty }D_{t}^{\alpha }\) represent the Liouville-Weyl fractional derivatives of order \(\frac{1}{2}< \alpha < 1\), \(L \in C(\mathbb {R}, \mathbb {R}^{N^2})\) is a symmetric matrix, and \(W \in C^{1}(\mathbb {R} \times \mathbb {R}^N, \mathbb {R})\). By applying the Fountain Theorem and the Dual Fountain Theorem, we demonstrate that this system admits two distinct sequences of solutions under the condition that L meets a new non-coercive criterion, and the potential W(t, x) exhibits combined nonlinearities.

考虑以下分数哈密顿系统：

这里， \(_{t}D_{\infty }^{\alpha }\)和\(_{-\infty }D_{t}^{\alpha }\)表示阶数为\的Liouville-Weyl分数导数(\frac{1}{2}< \alpha < 1\) , \(L \in C(\mathbb {R}, \mathbb {R}^{N^2})\)是对称矩阵，和\(W \in C^{1}(\mathbb {R} \times \mathbb {R}^N, \mathbb {R})\) 。通过应用喷泉定理和对偶喷泉定理，我们证明了该系统在L满足新的非强制准则且势W ( t , x ) 表现出组合非线性的条件下允许两个不同的解序列。