当前位置:
X-MOL 学术
›
J. Am. Chem. Soc.
›
论文详情
Our official English website, www.x-mol.net, welcomes your
feedback! (Note: you will need to create a separate account there.)
Isoreticular Curves: A Theory of Capillary Condensation To Model Water Sorption within Microporous Sorbents
Journal of the American Chemical Society ( IF 14.4 ) Pub Date : 2024-07-22 , DOI: 10.1021/jacs.4c02743 Julius J Oppenheim 1 , Mircea Dincǎ 1
Journal of the American Chemical Society ( IF 14.4 ) Pub Date : 2024-07-22 , DOI: 10.1021/jacs.4c02743 Julius J Oppenheim 1 , Mircea Dincǎ 1
Affiliation
|
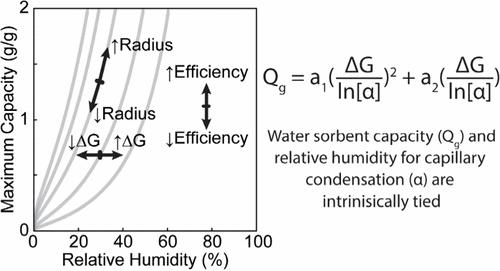
Metal–organic frameworks have gained traction as leading materials for water sorption applications due to precise chemical tunability of their well-ordered pores. These applications include atmospheric water capture, heat pumps, desiccation, desalination, humidity control, and thermal batteries. However, the relationships between the framework pore structure and the measurable water sorption properties, namely critical relative humidity for condensation, maximal capacity, and pore size or temperature for the onset of hysteresis, have not been clearly delineated. Herein, we precisely formulate these relationships by application of the theory of capillary condensation and macroscopic thermodynamic models to a large data set of MOF water isotherms. These relationships include a concept termed isoreticular curves that relates the critical pressure for pore condensation (α), gravimetric capacity (Qmax), and hydrophilicity (the Gibbs free energy for binding water, ΔG) as Qmax = a1(ΔG/ln α)2 + a2(ΔG/ln α), with constants a1 and a2 dependent upon the density and volume occupied by the linker and secondary building unit, and framework topology. Through this analysis, we propose guidelines for the maximization of sorption capacity at a given relative humidity with minimal hysteresis and discuss the theoretical limits for capacity at low relative humidity. This model provides an explanation for the lack of high-capacity frameworks at low relative humidity, as increasing pore size also causes an increase in relative humidity. We propose a loose upper bound of Qmax = −0.25(1/ln α)2 – 1.75(1/ln α) for the limit of maximal capacity at a given relative humidity in the dry regime. These guidelines are consequential for the design of new materials for water sorption applications.
中文翻译:

等网状曲线:模拟微孔吸附剂内水吸附的毛细管冷凝理论
由于其有序孔的精确化学可调性,金属有机框架作为吸水应用的主要材料而受到关注。这些应用包括大气水捕获、热泵、干燥、海水淡化、湿度控制和热电池。然而,框架孔隙结构和可测量的吸水特性(即冷凝的临界相对湿度、最大容量以及滞后开始的孔径或温度)之间的关系尚未明确描述。在这里,我们通过将毛细管冷凝理论和宏观热力学模型应用于大量 MOF 水等温线数据集,精确地表述了这些关系。这些关系包括一个称为等网曲线的概念,它将孔隙冷凝的临界压力 ( α )、重力容量 ( Q max ) 和亲水性(结合水的吉布斯自由能ΔG )联系起来,如下所示Q max = a 1 ( ΔG /ln α ) 2 + a 2 ( ΔG /ln α ),其中常数a 1和a 2取决于连接子和二级构建单元所占据的密度和体积以及框架拓扑。通过此分析,我们提出了在给定相对湿度下以最小滞后最大化吸附容量的指南,并讨论了低相对湿度下容量的理论极限。 该模型解释了低相对湿度下缺乏高容量框架的原因,因为孔径的增加也会导致相对湿度的增加。我们提出了一个宽松的上限Q max = −0.25(1/ln α) 2 – 1.75(1/ln α) 作为干燥状态下给定相对湿度下最大容量的限制。这些指南对于吸水应用新材料的设计非常重要。
更新日期:2024-07-22
中文翻译:

等网状曲线:模拟微孔吸附剂内水吸附的毛细管冷凝理论
由于其有序孔的精确化学可调性,金属有机框架作为吸水应用的主要材料而受到关注。这些应用包括大气水捕获、热泵、干燥、海水淡化、湿度控制和热电池。然而,框架孔隙结构和可测量的吸水特性(即冷凝的临界相对湿度、最大容量以及滞后开始的孔径或温度)之间的关系尚未明确描述。在这里,我们通过将毛细管冷凝理论和宏观热力学模型应用于大量 MOF 水等温线数据集,精确地表述了这些关系。这些关系包括一个称为等网曲线的概念,它将孔隙冷凝的临界压力 ( α )、重力容量 ( Q max ) 和亲水性(结合水的吉布斯自由能ΔG )联系起来,如下所示Q max = a 1 ( ΔG /ln α ) 2 + a 2 ( ΔG /ln α ),其中常数a 1和a 2取决于连接子和二级构建单元所占据的密度和体积以及框架拓扑。通过此分析,我们提出了在给定相对湿度下以最小滞后最大化吸附容量的指南,并讨论了低相对湿度下容量的理论极限。 该模型解释了低相对湿度下缺乏高容量框架的原因,因为孔径的增加也会导致相对湿度的增加。我们提出了一个宽松的上限Q max = −0.25(1/ln α) 2 – 1.75(1/ln α) 作为干燥状态下给定相对湿度下最大容量的限制。这些指南对于吸水应用新材料的设计非常重要。

















































 京公网安备 11010802027423号
京公网安备 11010802027423号