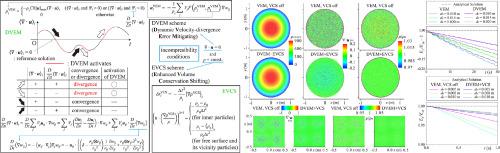
To the best knowledge of the authors, the numerical resolution of the continuity equation, i.e., the simultaneous achievement of accurate and physically consistent velocity divergence and density fields, has not been investigated in the context of projection-based particle methods. In this study, based on the Velocity-divergence Error Mitigating (VEM)/Volume Conservation Shifting (VCS) schemes developed for the WCSPH method, which improve the numerical resolution of the continuity equation, VEM/VCS schemes are proposed for projection-based particle methods. Furthermore, two other novel schemes are introduced. First, a Dynamic VEM (DVEM) scheme is proposed, where VEM is dynamically activated only when the velocity divergence instantaneously diverge from the reference solution at individual particles. The second scheme is referred to as Enhanced VCS by reference density (EVCS), where precise imposition of dynamic free surface boundary condition is considered. Several benchmark tests with different features have been conducted, and it is shown that the proposed schemes enhance the numerical resolution of the continuity equation for incompressible flows, i.e., the divergence free velocity and the constant density conditions. Application of DVEM and EVCS has provided enhanced resolution of the continuity equation along with clear reductions in the numerical energy dissipation associated with the approximated additional numerical terms.

中文翻译：

---

基于投影的 SPH 中连续性方程求解的增强方案


据作者所知，连续性方程的数值分辨率，即同时实现精确且物理一致的速度发散和密度场，尚未在基于投影的粒子方法的背景下进行研究。在本研究中，基于为 WCSPH 方法开发的速度发散误差减轻（VEM）/体积守恒移位（VCS）方案，提高了连续性方程的数值分辨率，提出了用于基于投影的粒子的 VEM/VCS 方案方法。此外，还介绍了另外两个新颖的方案。首先，提出了动态 VEM (DVEM) 方案，其中仅当单个粒子处的速度发散瞬时偏离参考解时，VEM 才会动态激活。第二种方案称为参考密度增强型 VCS (EVCS)，其中考虑了动态自由表面边界条件的精确施加。已经进行了几个具有不同特征的基准测试，结果表明，所提出的方案提高了不可压缩流连续性方程的数值分辨率，即无散度速度和恒定密度条件。 DVEM 和 EVCS 的应用提高了连续性方程的分辨率，并明显减少了与近似附加数值项相关的数值能量耗散。