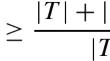
A directed diameter of a directed graph is the maximum possible distance between a pair of vertices, where paths must respect edge orientations, while undirected diameter is the diameter of the undirected graph obtained by symmetrizing the edges. In 2006 Babai proved that for a connected directed Cayley graph on \( n \) vertices the directed diameter is bounded above by a polynomial in undirected diameter and \( \log n \). Moreover, Babai conjectured that a similar bound holds for vertex-transitive graphs. We prove this conjecture of Babai, in fact, it follows from a more general bound for connected relations of homogeneous coherent configurations. The main novelty of the proof is a generalization of Ruzsa’s triangle inequality from additive combinatorics to the setting of graphs

有向图的有向直径是一对顶点之间的最大可能距离，其中路径必须尊重边方向，而无向直径是通过对称边获得的无向图的直径。 2006 年，Babai 证明，对于 \( n \) 个顶点上的连通有向凯莱图，有向直径的边界是无向直径和 \( \log n \) 的多项式。此外，巴拜推测类似的界限也适用于顶点传递图。我们证明了巴拜的这个猜想，事实上，它是从同质相干构型的连通关系的更一般的界限得出的。该证明的主要新颖之处在于将 Ruzsa 三角不等式从加性组合数学推广到图的设置