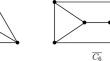
An injective edge-coloring of a graph G is an edge-coloring of G such that any two edges that are at distance 2 or in a common triangle receive distinct colors. The injective chromatic index of G is the minimum number of colors needed to guarantee that G admits an injective edge-coloring. Ferdjallah, Kerdjoudj and Raspaud showed that the injective chromatic index of every subcubic graph is at most 8, and conjectured that 8 can be improved to 6. Kostochka, Raspaud and Xu further proved that every subcubic graph has the injective chromatic index at most 7, and every subcubic planar graph has the injective chromatic index at most 6. In this paper, we consider the injective edge-coloring of claw-free subcubic graphs. We show that every connected claw-free subcubic graph, apart from two exceptions, has the injective chromatic index at most 5. We also consider the list version of injective edge-coloring and prove that the list injective chromatic index of every claw-free subcubic graph is at most 6. Both results are sharp and strengthen a recent result of Yang and Wu which asserts that every claw-free subcubic graph has the injective chromatic index at most 6.

图 G 的单射边缘着色是 G 的边缘着色，使得距离为 2 或位于公共三角形中的任意两条边接收不同的颜色。 G 的单射色指数是保证 G 允许单射边缘着色所需的最小颜色数。 Ferdjallah、Kerdjoudj 和 Raspaud 证明了每个次三次图的内射色指数至多为 8，并推测 8 可以提高到 6。Kostochka、Raspaud 和 Xu 进一步证明了每个次三次图的内射色指数至多为 7，并且每个次立方平面图的单射色指数最多为6。在本文中，我们考虑无爪次立方图的单射边着色。我们证明，除了两个例外之外，每个连通的无爪次立方图的单射色指数最多为 5。我们还考虑了单射边缘着色的列表版本，并证明了每个无爪次立方图的单射色指数图最多为 6。这两个结果都很尖锐，并强化了 Yang 和 Wu 最近的结果，该结果断言每个无爪次立方图的单射色指数最多为 6。