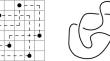
In 1977 Diaconis and Graham proved two inequalities relating different measures of disarray in permutations, and asked for a characterization of those permutations for which equality holds in one of these inequalities. Such a characterization was first given in 2013. Recently, another characterization was given by Woo, using a topological link in \({\mathbb {R}}^3\) that can be associated to the cycle diagram of a permutation. We show that Woo’s characterization extends much further: for any permutation, the discrepancy in Diaconis and Graham’s inequality is directly related to the Euler characteristic of the associated link. This connection provides a new proof of the original result of Diaconis and Graham. We also characterize permutations with a fixed discrepancy in terms of their associated links and find that the stabilized-interval-free permutations are precisely those whose associated links are nonsplit.

1977 年，迪亚科尼斯和格雷厄姆证明了两个不等式，它们与排列中不同的无序度量相关，并要求对这些排列的特征进行描述，这些排列在其中一个不等式中成立。这样的表征首次在 2013 年给出。最近，Woo 给出了另一个表征，使用了 \({\mathbb {R}}^3\) 中的拓扑链接，可以将其与排列的循环图相关联。我们表明，Woo 的表征延伸得更远：对于任何排列，戴科尼斯和格雷厄姆不等式的差异与相关联的欧拉特征直接相关。这种联系为戴康尼斯和格雷厄姆的原始结果提供了新的证明。我们还根据关联链接来描述具有固定差异的排列，并发现稳定的无区间排列正是关联链接不可分割的排列。