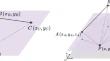
This paper introduces a novel method for solving the resection problem in two and three dimensions based on conformal geometric algebra (CGA). Advantage is taken because of the characteristics of CGA, which enables the representation of points, lines, planes, and volumes in a unified mathematical framework and offers a more intuitive and geometric understanding of the problem, in contrast to existing purely algebraic methods. Several numerical examples are presented to demonstrate the efficacy of the proposed method and to compare its validity with established techniques in the field. Numerical simulations indicate that our vector geometric algebra implementation is faster than the best-known algorithms to date, suggesting that the proposed GA-based methods can provide a more efficient and comprehensible solution to the two- and three-dimensional resection problem, paving the way for further applications and advances in geodesy research. Furthermore, the method’s emphasis on graphical and geometric representation makes it particularly suitable for educational purposes, allowing the reader to grasp the concepts and principles of resection more effectively. The proposed method has potential applications in a wide range of other fields, including surveying, robotics, computer vision, or navigation.

本文介绍了一种基于共形几何代数（CGA）的解决二维和三维交会问题的新方法。与现有的纯代数方法相比，CGA 的优势在于它能够在统一的数学框架中表示点、线、平面和体积，并提供对问题更直观和几何的理解。提出了几个数值示例来证明所提出方法的有效性，并将其有效性与该领域已建立的技术进行比较。数值模拟表明，我们的向量几何代数实现比迄今为止最知名的算法更快，这表明所提出的基于遗传算法的方法可以为二维和三维切除问题提供更有效和更容易理解的解决方案，从而铺平道路以获得大地测量学研究的进一步应用和进展。此外，该方法强调图形和几何表示，使其特别适合教育目的，使读者能够更有效地掌握切除的概念和原理。所提出的方法在其他广泛领域具有潜在的应用，包括测量、机器人、计算机视觉或导航。