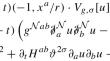
This paper is a part of a series devoted to the Euclidean-hyperboloidal foliation method introduced by the authors for investigating the global existence problem associated with nonlinear systems of coupled wave-Klein–Gordon equations with small data. This method was developed especially for investigating the initial value problem for the Einstein-massive field system in wave gauge. Here, we study the (fourth-order) field equations of f(R) modified gravity and investigate the global dynamical behavior of the gravitational field in the near-Minkowski regime. We establish the existence of a globally hyperbolic Cauchy development approaching Minkowski spacetime (in spacelike, null, and timelike directions), when the initial data set is sufficiently close to an asymptotically Euclidean and spacelike hypersurface in Minkowski spacetime. We cast the (fourth-order) f(R)-field equations in the form of a second-order wave-Klein–Gordon system, which has an analogous structure to the Einstein-massive field system but, in addition, involves a (possibly small) effective mass parameter. We establish the nonlinear stability of the Minkowski spacetime in the context of f(R) gravity, when the integrand f(R) in the action functional can be taken to be arbitrarily close to the integrand R of the standard Hilbert–Einstein action.

本文是作者介绍的欧几里德双曲面叶化方法系列文章的一部分，用于研究与小数据耦合波克莱因-戈登方程非线性系统相关的全局存在问题。该方法是专门为研究波规中爱因斯坦大质量场系统的初值问题而开发的。在这里，我们研究了 f(R) 修正引力的（四阶）场方程，并研究了近闵可夫斯基体系中引力场的全局动力学行为。当初始数据集足够接近闵可夫斯基时空中的渐近欧几里得和类空超曲面时，我们建立了接近闵可夫斯基时空（在类空、零和类时方向）的全局双曲柯西展开的存在。我们以二阶波克莱因-戈登系统的形式构建（四阶）f(R)场方程，该系统具有与爱因斯坦大质量场系统类似的结构，但此外还涉及（可能很小）有效质量参数。当作用函数中的被积函数 f(R) 可以任意接近标准希尔伯特-爱因斯坦作用的被积函数 R 时，我们在 f(R) 引力的背景下建立了闵可夫斯基时空的非线性稳定性。