当前位置:
X-MOL 学术
›
J. Chem. Theory Comput.
›
论文详情
Our official English website, www.x-mol.net, welcomes your
feedback! (Note: you will need to create a separate account there.)
Short-Time Infrequent Metadynamics for Improved Kinetics Inference
Journal of Chemical Theory and Computation ( IF 5.7 ) Pub Date : 2024-04-26 , DOI: 10.1021/acs.jctc.4c00170
Ofir Blumer 1 , Shlomi Reuveni 1, 2, 3 , Barak Hirshberg 1, 2, 3
Journal of Chemical Theory and Computation ( IF 5.7 ) Pub Date : 2024-04-26 , DOI: 10.1021/acs.jctc.4c00170
Ofir Blumer 1 , Shlomi Reuveni 1, 2, 3 , Barak Hirshberg 1, 2, 3
Affiliation
|
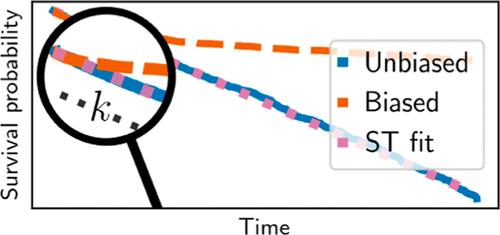
Infrequent Metadynamics is a popular method to obtain the rates of long time-scale processes from accelerated simulations. The inference procedure is based on rescaling the first-passage times of the Metadynamics trajectories using a bias-dependent acceleration factor. While useful in many cases, it is limited to Poisson kinetics, and a reliable estimation of the unbiased rate requires slow bias deposition and prior knowledge of efficient collective variables. Here, we propose an improved inference scheme, which is based on two key observations: (1) the time-independent rate of Poisson processes can be estimated using short trajectories only. (2) Short trajectories experience minimal bias, and their rescaled first-passage times follow the unbiased distribution even for relatively high deposition rates and suboptimal collective variables. Therefore, by basing the inference procedure on short time scales, we obtain an improved trade-off between speedup and accuracy at no additional computational cost, especially when employing suboptimal collective variables. We demonstrate the improved inference scheme for a model system and two molecular systems.
中文翻译:

用于改进动力学推理的短时罕见元动力学
罕见元动力学是一种从加速模拟中获取长时间尺度过程速率的流行方法。推理过程基于使用偏差相关加速因子重新调整 Metadynamics 轨迹的首次通过时间。虽然在许多情况下很有用,但它仅限于泊松动力学,并且对无偏率的可靠估计需要缓慢的偏差沉积和有效集体变量的先验知识。在这里,我们提出了一种改进的推理方案,该方案基于两个关键观察:(1)泊松过程的时间无关速率可以仅使用短轨迹来估计。 (2) 短轨迹的偏差最小,即使对于相对较高的沉积率和次优的集体变量,其重新调整的首次通过时间也遵循无偏分布。因此,通过将推理过程建立在短时间尺度上,我们可以在不增加计算成本的情况下获得加速率和准确性之间的改进权衡,特别是在使用次优集体变量时。我们展示了模型系统和两个分子系统的改进推理方案。
更新日期:2024-04-26
中文翻译:

用于改进动力学推理的短时罕见元动力学
罕见元动力学是一种从加速模拟中获取长时间尺度过程速率的流行方法。推理过程基于使用偏差相关加速因子重新调整 Metadynamics 轨迹的首次通过时间。虽然在许多情况下很有用,但它仅限于泊松动力学,并且对无偏率的可靠估计需要缓慢的偏差沉积和有效集体变量的先验知识。在这里,我们提出了一种改进的推理方案,该方案基于两个关键观察:(1)泊松过程的时间无关速率可以仅使用短轨迹来估计。 (2) 短轨迹的偏差最小,即使对于相对较高的沉积率和次优的集体变量,其重新调整的首次通过时间也遵循无偏分布。因此,通过将推理过程建立在短时间尺度上,我们可以在不增加计算成本的情况下获得加速率和准确性之间的改进权衡,特别是在使用次优集体变量时。我们展示了模型系统和两个分子系统的改进推理方案。































 京公网安备 11010802027423号
京公网安备 11010802027423号