A shift-splitting Jacobi-gradient iterative algorithm for solving the matrix equation A𝒱−𝒱‾B=C,Optimal Control Applications and Methods

当前位置： X-MOL 学术 › Optim. Control Appl. Methods › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

A shift-splitting Jacobi-gradient iterative algorithm for solving the matrix equation A𝒱−𝒱‾B=C
Optimal Control Applications and Methods ( IF 2.0 ) Pub Date : 2024-02-21 , DOI: 10.1002/oca.3112
Ahmed M. E. Bayoumi ₁

Affiliation

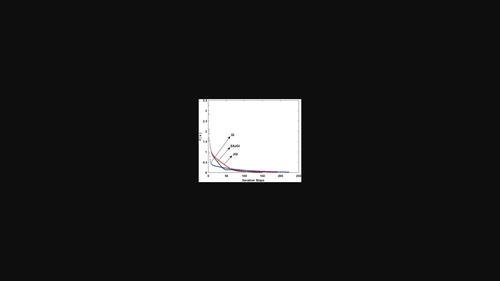
To improve the convergence of the gradient iterative (GI) algorithm and the Jacobi-gradient iterative (JGI) algorithm [Bayoumi, Appl Math Inf Sci, 2021], a shift-splitting Jacobi-gradient iterative (SSJGI) algorithm for solving the matrix equation

A 𝒱 - \overline{𝒱} B = C

is presented in this paper, which is based on the splitting of the coefficient matrices. The proposed algorithm converges to the exact solution for any initial value with some conditions. To demonstrate the effectiveness of the SSJGI algorithm and to compare it to the GI algorithm and the JGI algorithm [Bayoumi, Appl Math Inf Sci, 2021], numerical examples are provided.

中文翻译：