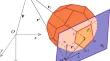
For polyhedral mass bodies having arbitrary shape and density distribution of polynomial type we present a tensorial approach to derive analytical expressions of the gravitational potential and gravity vector. They are evaluated at an arbitrary point by means of formulas, referred to a Cartesian reference frame having an arbitrary origin, that are shown to be singularity-free whatever is the position of the observation point with respect to the body. The solution is expressed as a sum of algebraic quantities depending solely upon the 3D coordinates of the polyhedron vertices and the coefficients of the polynomial density function. Hence, no recursive expression needs to be invoked as in the recent contribution by Ren et al. (Surv Geophys 41:695–722, 2020). Moreover, the tensorial formalism developed in the paper allows one to obtain more concise, coordinate-free expressions that can also be extended to address polynomial functions of greater order. The analytical expressions of the gravitational potential and gravity vector are numerically validated and compared with alternative methods retrieved from the literature.

对于具有任意形状和多项式类型密度分布的多面体质量体，我们提出了一种张量方法来推导重力势和重力矢量的解析表达式。它们通过公式在任意点进行评估，参考具有任意原点的笛卡尔参考系，无论观察点相对于物体的位置如何，这些公式都显示为无奇点。该解表示为仅取决于多面体顶点的 3D 坐标和多项式密度函数的系数的代数量之和。因此，不需要像 Ren 等人最近的贡献那样调用递归表达式。 (Surv Geophys 41:695–722, 2020)。此外，本文提出的张量形式允许人们获得更简洁、无坐标的表达式，这些表达式也可以扩展到解决更高阶的多项式函数。重力势和重力矢量的解析表达式经过数值验证，并与从文献中检索到的替代方法进行了比较。