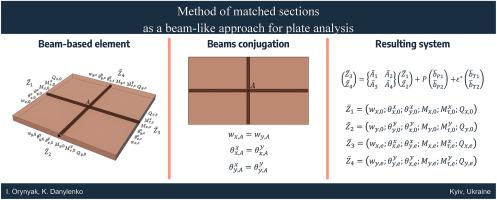
A new numerical method in application to the plate problem is suggested. It starts from consideration of the rectangular elements, each operating by 6 beam-like parameters: four bending parameters (displacement, angle of rotation, bending moment, transverse force) and two rotation parameters (angle of rotation and twisting moment). So, contrary to the classical FEM approach, the conjugation between the adjacent elements occurs between the adjacent sections rather than in polygon vertexes (nodes), and this gives the name to the method – method of matched sections, MMS. Technically, 6 left-side and 6 lower-side parameters are 12 inlet parameters, while 6 upper-side and right-side parameters are 12 outlet parameters; each element is defined by 24 parameters. Outlet parameters are related to inlet ones by 12 matrix relations, which are derived from the approximate solution of each differential equation (equilibrium, physical, and geometrical equations) of the plate theory. The matrix relation between inlet and outlet parameters is written in a form suitable for applying the transfer matrix method. The numerical examples for the thin and Mindlin plates show the high efficiency and accuracy of the method. In particular, the results for the Mindlin plate for minimal thickness give the same results as the thin plate (no shear locking); the method is insensitive to cases when, for adjacent elements, the ratio of dimensions or ratio of rigidities (elastic constants) differ by several orders of magnitude. The application of the method for the thermal as well as for the vibration problem is considered. The possible extension of the method to any curved geometry is discussed, too.

A 提出了应用于板问题的新数值方法。它从考虑矩形单元开始，每个矩形单元由 6 个类梁参数操作：四个弯曲参数（位移、旋转角度、弯矩、横向力）和两个旋转参数（旋转角度和扭转力矩）。因此，与经典的 FEM 方法相反，相邻单元之间的共轭发生在相邻截面之间，而不是在多边形顶点（节点）中，这就是该方法的名称 - 匹配截面方法，MMS。从技术上讲，左侧6个、下侧6个参数是12个入口参数，而上侧和右侧6个参数是12个出口参数；每个元素由 24 个参数定义。出口参数与入口参数之间存在12个矩阵关系，这些矩阵关系是由板理论各微分方程（平衡方程、物理方程和几何方程）的近似解导出的。入口和出口参数之间的矩阵关系以适合应用传递矩阵方法的形式编写。薄板和Mindlin板的数值算例表明了该方法的高效性和准确性。特别是，最小厚度的 Mindlin 板的结果与薄板的结果相同（无剪切锁定）；该方法对于相邻单元的尺寸比或刚度比（弹性常数）相差几个数量级的情况不敏感。考虑了该方法在热问题和振动问题中的应用。还讨论了将该方法扩展到任何弯曲几何形状的可能。