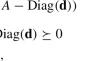
We study several variants of decomposing a symmetric matrix into a sum of a low-rank positive-semidefinite matrix and a diagonal matrix. Such decompositions have applications in factor analysis, and they have been studied for many decades. On the one hand, we prove that when the rank of the positive-semidefinite matrix in the decomposition is bounded above by an absolute constant, the problem can be solved in polynomial time. On the other hand, we prove that, in general, these problems as well as their certain approximation versions are all NP-hard. Finally, we prove that many of these low-rank decomposition problems are complete in the first-order theory of the reals, i.e., given any system of polynomial equations, we can write down a low-rank decomposition problem in polynomial time so that the original system has a solution iff our corresponding decomposition problem has a feasible solution of certain (lowest) rank.

我们研究了将对称矩阵分解为低秩正半定矩阵和对角矩阵之和的几种变体。这种分解在因子分析中得到应用，并且已经被研究了几十年。一方面，我们证明当分解中正半定矩阵的秩以绝对常数为界时，问题可以在多项式时间内求解。另一方面，我们证明，一般来说，这些问题以及它们的某些近似版本都是 NP 困难的。最后，我们证明许多低秩分解问题在实数的一阶理论中是完备的，即给定任何多项式方程组，我们可以在多项式时间内写出一个低秩分解问题，使得原始系统有一个解，当且仅当我们相应的分解问题有某个（最低）秩的可行解。