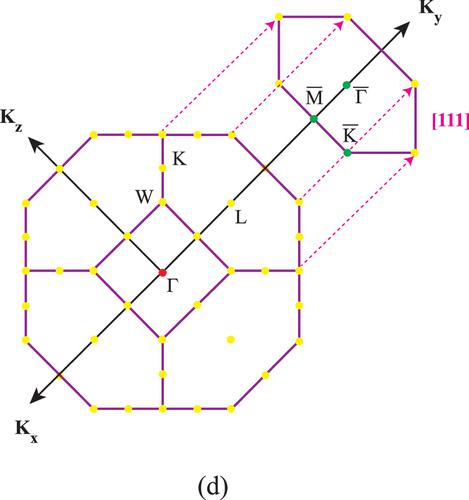
We correct some labeling errors in the figures and provide the corrected figures. We sincerely apologize for any inconvenience caused because of the inadvertent mistake. This does not affect the results or conclusions described in the paper. In the main manuscript Figure 1d, K_x, K_y, and K_z vectors are not orthogonal, which leads to the misconception in another figure. The corrected figure is provided here. In the corrected figure, the projected (111) Brillouin zone is shown with a bar over a high symmetric point which is used in the surface notation (which was previously missing). In the corrected figure, K_x, K_y, and K_z directions are orthogonal and they are coming out of the square sides. Figure 1. (d) Brillouin zone of bulk AgCaAs and projected hexagonal Brillouin zone with the high symmetric points 2D AgCaAs. In Figure 7a, we use K₁, K₂, and K₃ notation in Wannier charge center evolution. The ${\mathbb{Z}}_2$ invariant can be obtained by calculating the Wilson loop for the six-time-reversal invariant momentum plane. Since we use K_x, K_y, and K_z in Figure 1d, the corresponding change has been made in Figure 7a to K_x, K_y, and K_z notation. The corresponding six planes are K_x = 0.0, K_x = 0.5; K_y = 0.0, K_y = 0.5; and K_z = 0.0, K_z = 0.5. Figure 7. (a) Evolution of the Wannier charge centered along the six time-reversal invariant momenta points. (b) Variation of the energy gap at the Γ point due to the biaxial strain. The yellow and blue regions indicate the normal insulating and topological insulating phases respectively (c) Evolution of the ${\mathbb{Z}}_2$ invariant with biaxial strain. (d) Surface band structure representing conducting surface. (e) Slab band structure. We used the (111) surface to calculate surface and slab band structure of bulk AgCaAs. We use X as the general notation in Figure 7d,e, which was not corrected. Since we calculate the surface state along the −M̅− Γ̅−M̅ path, we change it in Figure 7d,e. The conducting surface states are protected by the material’s topological properties, making them robust against disorder and impurities. The conducting surface means “states can emerge within the bulk band gap”, which is responsible for transportation. We can also find the top and bottom surface bands different (in Figure 7e) because in the system different terminations are possible. If there are dangling bonds on the surface, there will be possibilities to get different slab band structures due to the different TB models constructed from MLWFs (even though the band structures are the same). Here we use the top surface in the calculations of the surface band structure. In 2D AgCaAs, we calculated that the topological properties happen in the K_z = 0.0 plane only, because the 2D compound is just a layer structured 3D compound with a vacuum along the K_z direction. We calculated edge states of 2D AgCaAs on the (100) surface which has the X point in their orthorhombic Brillouin zone (similar to the MoS₂). We calculate the surface state along the −X̅− Γ̅−X̅ path and the corresponding label has been changed in Figure 8b,c. Figure 8. (a) Evolution of the Wannier charge centered in 2D AgCaAs. (b) Conducting edge states. (c) Slab band structure indicating gapless edges. This article has not yet been cited by other publications. Figure 1. (d) Brillouin zone of bulk AgCaAs and projected hexagonal Brillouin zone with the high symmetric points 2D AgCaAs. Figure 7. (a) Evolution of the Wannier charge centered along the six time-reversal invariant momenta points. (b) Variation of the energy gap at the Γ point due to the biaxial strain. The yellow and blue regions indicate the normal insulating and topological insulating phases respectively (c) Evolution of the ${\mathbb{Z}}_2$ invariant with biaxial strain. (d) Surface band structure representing conducting surface. (e) Slab band structure. Figure 8. (a) Evolution of the Wannier charge centered in 2D AgCaAs. (b) Conducting edge states. (c) Slab band structure indicating gapless edges.

中文翻译：

---

对“AgCaAs Heusler 合金中具有优异催化活性的拓扑相变的证据：第一性原理研究”的修正

我们纠正了图中的一些标签错误并提供了更正后的数字。对于因无意错误而造成的任何不便，我们深表歉意。这并不影响论文中描述的结果或结论。在主稿图 1d 中，K _x、K _y和K _z向量不是正交的，这导致了另一幅图中的误解。此处提供了修正后的数字。在校正后的图中，投影的 (111) 布里渊区在高对称点上显示为条形，该点用于表面符号（之前缺失）。在校正后的图中，K _x、K _y和K _z方向是正交的，并且它们从正方形边出来。图 1. (d) 大块 AgCaAs 的布里渊区和具有高对称点的二维 AgCaAs 投影六边形布里渊区。在图7a中，我们在Wannier电荷中心演化中使用K ₁、K ₂和K _3符号。这${\mathbb{Z}}_2$不变量可以通过计算六次反转不变量动量平面的威尔逊环来获得。由于我们在图 1d 中使用K _x、K _y和K _z ，因此图 7a 中的K _x、K _y和K _z表示法也进行了相应的更改。对应的六个平面分别为K _x = 0.0、K _x = 0.5；Ky _{= 0.0}，Ky = 0.5；且Kz ₌ 0.0，Kz = 0.5 _。图 7.(a) Wannier 电荷的演化以六个时间反转不变动量点为中心。(b) 双轴应变引起的 Γ 点能隙的变化。黄色和蓝色区域分别表示正常绝缘相和拓扑绝缘相 (c) 的演化${\mathbb{Z}}_2$双轴应变不变。(d) 代表导电表面的表面能带结构。(e) 板带结构。我们使用 (111) 表面来计算块状 AgCaAs 的表面和板条能带结构。我们使用 X 作为图 7d、e 中的通用符号，该符号未进行更正。由于我们沿着 − M̅ − Ѕ− M̅路径计算表面状态，因此我们在图 7d、e 中对其进行了更改。导电表面态受到材料拓扑特性的保护，使其能够抵抗无序和杂质。导电表面意味着“状态可以在体带隙内出现”，它负责传输。我们还可以发现顶部和底部表面带不同（如图 7e 所示），因为系统中可能有不同的终端。如果表面存在悬空键，由于 MLWF 构建的 TB 模型不同（即使能带结构相同），就有可能获得不同的板能带结构。这里我们在表面能带结构的计算中使用顶面。在 2D AgCaAs 中，我们计算出拓扑性质仅发生在K _z = 0.0 平面中，因为 2D 化合物只是沿K _z方向具有真空的层状结构 3D 化合物。我们计算了 (100) 表面上二维 AgCaAs 的边缘态，其 X 点位于正交布里渊区（类似于 MoS ₂）。我们沿着 − X̅ − Γ̅− X̅路径计算表面状态，并且相应的标签在图 8b、c 中已更改。图 8.(a) 以 2D AgCaAs 为中心的 Wannier 电荷的演化。(b) 传导边缘态。(c) 板带结构表明无间隙边缘。这篇文章尚未被其他出版物引用。图 1. (d) 大块 AgCaAs 的布里渊区和具有高对称点的二维 AgCaAs 投影六边形布里渊区。图 7.(a) Wannier 电荷的演化以六个时间反转不变动量点为中心。(b) 双轴应变引起的 Γ 点能隙的变化。黄色和蓝色区域分别表示正常绝缘相和拓扑绝缘相 (c) 的演化${\mathbb{Z}}_2$双轴应变不变。(d) 代表导电表面的表面能带结构。(e) 板带结构。图 8.(a) 以 2D AgCaAs 为中心的 Wannier 电荷的演化。(b) 传导边缘态。(c) 板带结构表明无间隙边缘。