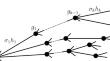
For any countable group with infinite conjugacy classes we construct a family of forests on the group. For each of them there is a random walk on the group with the property that its sample paths almost surely converge to the geometric boundary of the forest in a way that resembles the simple random walks on trees. It allows us to identify the Poisson boundary of the random walk with the boundary of the forest and to show that the group action on the Poisson boundary is free (which, in particular, implies non-triviality of the Poisson boundary). As a consequence we obtain that any countable group carries a random walk such that the stabilizer of almost every point of the Poisson boundary coincides with the hyper-FC-centre of the group, and, more generally, we characterize all normal subgroups which can serve as the pointwise stabilizer of the Poisson boundary of a random walk on a given countable group. Our work is a development of a recent result of Frisch–Hartman–Tamuz–Vahidi Ferdowsi who proved that any group which is not hyper-FC-central admits a measure with a non-trivial Poisson boundary.

对于任何具有无限共轭类的可数群，我们在该群上构造一个森林族。对于它们中的每一个，组上都有一个随机游走，其样本路径几乎肯定会以类似于树上的简单随机游走的方式收敛到森林的几何边界。它使我们能够将随机游走的泊松边界与森林边界进行识别，并证明泊松边界上的群作用是自由的（特别是，这意味着泊松边界的非平凡性）。因此，我们得到任何可数群都具有随机游走，使得泊松边界的几乎每个点的稳定器与该群的超 FC 中心重合，并且更一般地，我们描述了可以服务的所有正常子群作为给定可数群上随机游走的泊松边界的点稳定器。我们的工作是 Frisch-Hartman-Tamuz-Vahidi Ferdowsi 最近结果的发展，证明任何不是超 FC 中心的群都承认具有非平凡泊松边界的测度。