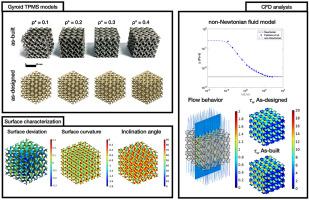
在医学工程领域,三周期最小表面 (TPMS) 结构因其物理属性与人体骨骼相似而被广泛研究。计算流体动力学 (CFD) 通常用于揭示结构架构和流场之间的相互作用。然而,仍然缺乏关于制造缺陷和非牛顿行为对 TPMS 支架中流体响应影响的全面研究。因此,本研究制造了具有从 0.1 到 0.4 的四种相对密度的 Gyroid TPMS。使用无损技术检查表面粗糙度和几何偏差。我们发现制造缺陷对液体反应的影响很小。含缺陷模型和无缺陷模型之间的压降比较可能相差高达 7%。平均剪切应力的相同比较显示差异高达 23%,其中在较高的相对密度下观察到两种模型之间的偏差更大。相反,黏度模型在流动预测中起着重要作用。通过将牛顿模型与 Carreau-Yasuda 非牛顿模型进行比较,非牛顿粘度产生的压降和平均壁面剪切应力可能比牛顿模型高两倍以上。此外,我们将来自两种粘度模型的流体诱导剪切应力与从文献中获得的组织生长的理想剪切应力范围相匹配。牛顿模型中高达 70% 的应力落在理想范围内,而非牛顿结果的匹配应力降低到低于 8%。 此外,通过将几何特征与物理输出相关联,可以看到几何偏差与表面曲率相关,而局部剪切应力则显示出与倾角的强相关性。总体而言,本研究强调了粘度模型对支架 CFD 分析的重要性,尤其是当产生的流体诱导壁剪切应力感兴趣时。此外,几何相关性引入了从局部角度对结构结构的替代考虑,这可能有助于未来不同多孔支架之间的进一步比较和优化。
 "点击查看英文标题和摘要"
"点击查看英文标题和摘要"
Assessing the effect of manufacturing defects and non-Newtonian blood model on flow behaviors of additively manufactured Gyroid TPMS structures
In the field of medical engineering, Triply Periodic Minimal Surfaces (TPMS) structures have been studied widely owing to their physical attributes similar to those of human bones. Computational Fluid Dynamics (CFD) is often used to reveal the interaction between structural architectures and flow fields. Nevertheless, a comprehensive study on the effect of manufacturing defects and non-Newtonian behavior on the fluid responses in TPMS scaffolds is still lacking. Therefore, the present study fabricated Gyroid TPMS with four relative densities from 0.1 to 0.4. Non-destructive techniques were used to examine surface roughness and geometric deviation. We found that the manufacturing defects had a minor effect on fluid responses. The pressure drop comparison between defect-containing and defect-free models could be differed up to 7%. The same comparison for the average shear stress showed a difference up to 23%, in which greater deviation between both models was observed at higher relative density. On the contrary, the viscosity model played a significant role in flow prediction. By comparing the Newtonian model with Carreau-Yasuda non-Newtonian model, the resulting pressure drop and average wall shear stress from non-Newtonian viscosity could be higher than those of the Newtonian model by more than a factor of two. In addition, we matched the fluid-induced shear stress from both viscosity models with desirable ranges of shear stresses for tissue growth obtained from the literature. Up to 70% from the Newtonian model fell within the desirable range while the matching stress reduced to lower than 8% for the non-Newtonian results. Furthermore, by correlating geometric features with physical outputs, the geometric deviation was seen associated with surface curvature while the local shear stress revealed a strong correlation with inclination angle. Overall, the present work emphasized the importance of the viscosity model for CFD analysis of the scaffolds, especially when resulting fluid-induced wall shear stress is of interest. In addition, the geometric correlation has introduced the alternative consideration of structural architectures from local perspectives, which could assist the further comparison and optimization among different porous scaffolds in the future.


































 京公网安备 11010802027423号
京公网安备 11010802027423号