Acta Numerica ( IF 16.3 ) Pub Date : 2022-06-09 , DOI: 10.1017/s0962492922000034 Martin J. Gander , Hui Zhang
Schwarz methods use a decomposition of the computational domain into subdomains and need to impose boundary conditions on the subdomain boundaries. In domain truncation one restricts the unbounded domain to a bounded computational domain and must also put boundary conditions on the computational domain boundaries. In both fields there are vast bodies of literature and research is very active and ongoing. It turns out to be fruitful to think of the domain decomposition in Schwarz methods as a truncation of the domain onto subdomains. Seminal precursors of this fundamental idea are papers by Hagstrom, Tewarson and Jazcilevich (1988), Després (1990) and Lions (1990). The first truly optimal Schwarz method that converges in a finite number of steps was proposed by Nataf (1993), and used precisely transparent boundary conditions as transmission conditions between subdomains. Approximating these transparent boundary conditions for fast convergence of Schwarz methods led to the development of optimized Schwarz methods – a name that has become common for Schwarz methods based on domain truncation. Compared to classical Schwarz methods, which use simple Dirichlet transmission conditions and have been successfully used in a wide range of applications, optimized Schwarz methods are much less well understood, mainly due to their more sophisticated transmission conditions.
A key application of Schwarz methods with such sophisticated transmission conditions turned out to be time-harmonic wave propagation problems, because classical Schwarz methods simply do not work in this case. The past decade has given us many new Schwarz methods based on domain truncation. One review from an algorithmic perspective (Gander and Zhang 2019) showed the equivalence of many of these new methods to optimized Schwarz methods. The analysis of optimized Schwarz methods, however, is lagging behind their algorithmic development. The general abstract Schwarz framework cannot be used for the analysis of these methods, and thus there are many open theoretical questions about their convergence. Just as for practical multigrid methods, Fourier analysis has been instrumental for understanding the convergence of optimized Schwarz methods and for tuning their transmission conditions. Similar to local Fourier mode analysis in multigrid, the unbounded two-subdomain case is used as a model for Fourier analysis of optimized Schwarz methods due to its simplicity. Many aspects of the actual situation, e.g. boundary conditions of the original problem and the number of subdomains, were thus neglected in the unbounded two-subdomain analysis. While this gave important insight, new phenomena beyond the unbounded two-subdomain models were discovered.
This present situation is the motivation for our survey: to give a comprehensive review and precise exploration of convergence behaviours of optimized Schwarz methods based on Fourier analysis, taking into account the original boundary conditions, many-subdomain decompositions and layered media. We consider as our model problem the operator
$-\Delta + \eta $
 in the diffusive case
$\eta>0$
in the diffusive case
$\eta>0$
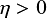 (screened Laplace equation) or the oscillatory case
$\eta <0$
(screened Laplace equation) or the oscillatory case
$\eta <0$
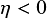 (Helmholtz equation), in order to show the fundamental difference in behaviour of Schwarz solvers for these problems. The transmission conditions we study include the lowest-order absorbing conditions (Robin), and also more advanced perfectly matched layers (PMLs), both developed first for domain truncation. Our intensive work over the last two years on this review has led to several new results presented here for the first time: in the bounded two-subdomain analysis for the Helmholtz equation, we see strong influence of the original boundary conditions imposed on the global problem on the convergence factor of the Schwarz methods, and the asymptotic convergence factors with small overlap can differ from the unbounded two-subdomain analysis. In the many-subdomain analysis, we find the scaling with the number of subdomains, e.g. when the subdomain size is fixed, robust convergence of the double-sweep Schwarz method for the free-space wave problem, either with fixed overlap and zeroth-order Taylor conditions or with a logarithmically growing PML, and we find that Schwarz methods with PMLs work like smoothers that converge faster for higher Fourier frequencies; in particular, for the free-space wave problem, plane waves (in the error) passing through interfaces at a right angle converge more slowly. In addition to our main focus on analysis in Sections 2 and 3, we start in Section 1 with an expository historical introduction to Schwarz methods, and in Section 4 we give a brief interpretation of the recently proposed optimal Schwarz methods for decompositions with cross-points from the viewpoint of transmission conditions. We conclude in Section 5 with a summary of open research problems. In Appendix A we provide a Matlab program for a block LU form of an optimal Schwarz method with cross-points, and in Appendix B we give the Maple program for the two-subdomain Fourier analysis.
(Helmholtz equation), in order to show the fundamental difference in behaviour of Schwarz solvers for these problems. The transmission conditions we study include the lowest-order absorbing conditions (Robin), and also more advanced perfectly matched layers (PMLs), both developed first for domain truncation. Our intensive work over the last two years on this review has led to several new results presented here for the first time: in the bounded two-subdomain analysis for the Helmholtz equation, we see strong influence of the original boundary conditions imposed on the global problem on the convergence factor of the Schwarz methods, and the asymptotic convergence factors with small overlap can differ from the unbounded two-subdomain analysis. In the many-subdomain analysis, we find the scaling with the number of subdomains, e.g. when the subdomain size is fixed, robust convergence of the double-sweep Schwarz method for the free-space wave problem, either with fixed overlap and zeroth-order Taylor conditions or with a logarithmically growing PML, and we find that Schwarz methods with PMLs work like smoothers that converge faster for higher Fourier frequencies; in particular, for the free-space wave problem, plane waves (in the error) passing through interfaces at a right angle converge more slowly. In addition to our main focus on analysis in Sections 2 and 3, we start in Section 1 with an expository historical introduction to Schwarz methods, and in Section 4 we give a brief interpretation of the recently proposed optimal Schwarz methods for decompositions with cross-points from the viewpoint of transmission conditions. We conclude in Section 5 with a summary of open research problems. In Appendix A we provide a Matlab program for a block LU form of an optimal Schwarz method with cross-points, and in Appendix B we give the Maple program for the two-subdomain Fourier analysis.
中文翻译:

通过域截断的 Schwarz 方法
Schwarz 方法使用将计算域分解为子域,并且需要在子域边界上施加边界条件。在域截断中,将无界域限制为有界计算域,并且还必须在计算域边界上放置边界条件。在这两个领域都有大量的文献,研究非常活跃和持续。将 Schwarz 方法中的域分解视为将域截断为子域,结果证明是富有成效的。这一基本思想的开创性先驱是 Hagstrom、Tewarson 和 Jazcilevich (1988)、Després (1990) 和 Lions (1990) 的论文。Nataf (1993) 提出了第一个在有限步内收敛的真正最优 Schwarz 方法,并使用精确透明的边界条件作为子域之间的传输条件。逼近这些透明边界条件以实现 Schwarz 方法的快速收敛,导致优化 Schwarz 方法的发展——这个名称已成为基于域截断的 Schwarz 方法的常见名称。与使用简单的狄利克雷传输条件并已成功用于广泛应用的经典 Schwarz 方法相比,优化的 Schwarz 方法的理解要少得多,主要是由于其更复杂的传输条件。
Schwarz 方法在如此复杂的传输条件下的一个关键应用是时谐波传播问题,因为经典的 Schwarz 方法在这种情况下根本不起作用。过去十年为我们提供了许多基于域截断的新 Schwarz 方法。从算法角度进行的一项评论(Gander 和 Zhang 2019)显示了许多这些新方法与优化的 Schwarz 方法等价。然而,优化 Schwarz 方法的分析落后于它们的算法发展。一般抽象的 Schwarz 框架不能用于分析这些方法,因此关于它们的收敛性存在许多开放的理论问题。就像实用的多重网格方法一样,傅立叶分析有助于理解优化 Schwarz 方法的收敛性和调整其传输条件。类似于多重网格中的局部傅里叶模式分析,由于其简单性,无界二子域情况被用作优化 Schwarz 方法的傅里叶分析模型。多方面的实际情况,例如,原始问题的边界条件和子域的数量,因此在无界二子域分析中被忽略。虽然这提供了重要的见解,但发现了无界两个子域模型之外的新现象。
这种现状是我们调查的动机:对基于傅里叶分析的优化 Schwarz 方法的收敛行为进行全面审查和精确探索,同时考虑到原始边界条件、多子域分解和分层媒体。我们将扩散情况
$\eta>0$
(屏蔽拉普拉斯方程)或振荡情况
$\eta <0$
中的算子
$-\Delta + \eta $
 视为我们的模型问题
视为我们的模型问题
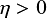
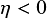 (亥姆霍兹方程),以显示施瓦茨求解器对这些问题的行为的根本差异。我们研究的传输条件包括最低阶吸收条件 (Robin),以及更高级的完美匹配层 (PML),它们都是首先为域截断而开发的。在过去两年中,我们在本次审查中的密集工作首次在此提出了几个新结果:在亥姆霍兹方程的有界二子域分析中,我们看到原始边界条件对全局问题的强烈影响关于 Schwarz 方法的收敛因子,具有小重叠的渐近收敛因子可以不同于无界二子域分析。在多子域分析中,我们发现随着子域数量的缩放,例如当子域大小固定时,自由空间波问题的双扫描 Schwarz 方法的稳健收敛,无论是具有固定重叠和零阶泰勒条件还是具有对数增长的 PML,我们发现具有 PML 的 Schwarz 方法有效比如平滑器,对于更高的傅里叶频率收敛更快;特别是对于自由空间波问题,平面波(在误差中)以直角通过界面会收敛得更慢。除了我们在第 2 节和第 3 节中主要关注分析之外,我们从第 1 节开始对 Schwarz 方法进行说明性历史介绍,在第 4 节中,我们简要解释了最近提出的用于交叉点分解的最优 Schwarz 方法从传输条件来看。我们在第 5 节总结了开放的研究问题。在附录 A 中,我们提供了一个带有交叉点的最优 Schwarz 方法的块 LU 形式的 Matlab 程序,在附录 B 中,我们给出了用于两个子域傅里叶分析的 Maple 程序。
(亥姆霍兹方程),以显示施瓦茨求解器对这些问题的行为的根本差异。我们研究的传输条件包括最低阶吸收条件 (Robin),以及更高级的完美匹配层 (PML),它们都是首先为域截断而开发的。在过去两年中,我们在本次审查中的密集工作首次在此提出了几个新结果:在亥姆霍兹方程的有界二子域分析中,我们看到原始边界条件对全局问题的强烈影响关于 Schwarz 方法的收敛因子,具有小重叠的渐近收敛因子可以不同于无界二子域分析。在多子域分析中,我们发现随着子域数量的缩放,例如当子域大小固定时,自由空间波问题的双扫描 Schwarz 方法的稳健收敛,无论是具有固定重叠和零阶泰勒条件还是具有对数增长的 PML,我们发现具有 PML 的 Schwarz 方法有效比如平滑器,对于更高的傅里叶频率收敛更快;特别是对于自由空间波问题,平面波(在误差中)以直角通过界面会收敛得更慢。除了我们在第 2 节和第 3 节中主要关注分析之外,我们从第 1 节开始对 Schwarz 方法进行说明性历史介绍,在第 4 节中,我们简要解释了最近提出的用于交叉点分解的最优 Schwarz 方法从传输条件来看。我们在第 5 节总结了开放的研究问题。在附录 A 中,我们提供了一个带有交叉点的最优 Schwarz 方法的块 LU 形式的 Matlab 程序,在附录 B 中,我们给出了用于两个子域傅里叶分析的 Maple 程序。






























 京公网安备 11010802027423号
京公网安备 11010802027423号