Detailed Analysis of the Ice Surface after Binding of an Insect Antifreeze Protein and Correlation with the Gibbs–Thomson Equation,Langmuir

当前位置： X-MOL 学术 › Langmuir › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

Detailed Analysis of the Ice Surface after Binding of an Insect Antifreeze Protein and Correlation with the Gibbs–Thomson Equation
Langmuir ( IF 3.7 ) Pub Date : 2021-09-29 , DOI: 10.1021/acs.langmuir.1c01620
Julian Gerhäuser ₁ , Volker Gaukel ₁

Affiliation

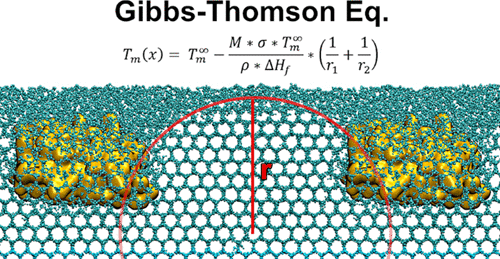
Antifreeze proteins (AFPs) are able to influence the ice crystal growth and the recrystallization process due to the Gibbs–Thomson effect. The binding of the AFP leads to the formation of a curved ice surface and it is generally assumed that there is a critical radius between the proteins on the ice surface that determines the maximal thermal hysteresis. Up to now, this critical radius has not yet been proven beyond doubt or only in poor agreement with the Gibbs–Thomson equation. Using molecular dynamics (MD) simulations, the resulting three-dimensional surface structure is analyzed and the location of the critical radius is identified. Our results demonstrate that the correct analysis of the geometry of the ice surface is extremely important and cannot be guessed upfront a simulation. In contrary to earlier expectations from the literature, we could show that the critical radius is not located directly between the adsorbed proteins. In addition, we showed that the minimum temperature at which the system does not freeze is in very good agreement with the value calculated with the Gibbs–Thomson equation at the critical radius, as long as dynamic system conditions are taken into account. This proves on the one hand that the Gibbs–Thomson effect is the basis of thermal hysteresis and that MD simulations are suitable for the prediction of the melting point depression.

中文翻译：

结合昆虫抗冻蛋白后冰面的详细分析以及与 Gibbs-Thomson 方程的相关性

由于吉布斯-汤姆森效应，抗冻蛋白 (AFP) 能够影响冰晶生长和重结晶过程。AFP 的结合导致形成弯曲的冰面，通常假设冰面上的蛋白质之间存在临界半径，这决定了最大的热滞后。到目前为止，这个临界半径还没有被证明是毫无疑问的，或者与吉布斯-汤姆森方程的一致性很差。使用分子动力学 (MD) 模拟，分析所得的三维表面结构并确定临界半径的位置。我们的结果表明，对冰面几何形状的正确分析非常重要，并且无法在模拟之前猜测。与先前文献中的预期相反，我们可以证明临界半径并不直接位于吸附的蛋白质之间。此外，我们表明，只要考虑到动态系统条件，系统不会冻结的最低温度与临界半径处的 Gibbs-Thomson 方程计算值非常吻合。这一方面证明了 Gibbs-Thomson 效应是热滞后的基础，并且 MD 模拟适用于预测熔点下降。只要考虑到动态系统条件。这一方面证明了 Gibbs-Thomson 效应是热滞后的基础，并且 MD 模拟适用于预测熔点下降。只要考虑到动态系统条件。这一方面证明了 Gibbs-Thomson 效应是热滞后的基础，并且 MD 模拟适用于预测熔点下降。

更新日期：2021-10-12

点击分享查看原文

点击收藏

阅读更多本刊新发论文本刊介绍/投稿指南